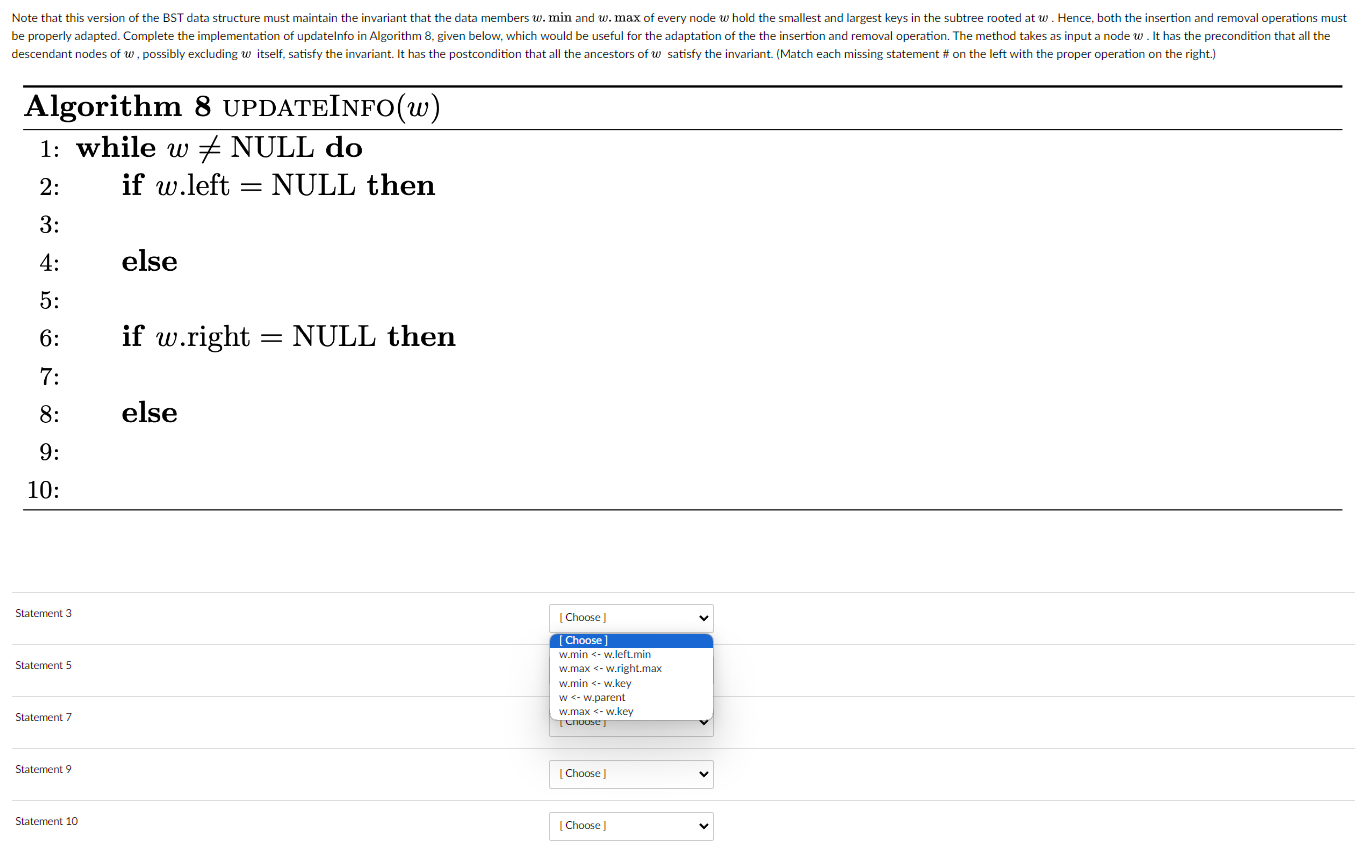
Consider a version of a binary search tree (BST) for sorted maps that stores additional information as data members of each node w of the tree to account for the smallest and largest keys in the subtree rooted at w. Suppose that we can access this information using w. min, for the smallest integer key, and w.max, for the largest. Algorithm 6 (Node), given below, provides the pseudocode for the constructor of a node in a binary tree with the additional information. Algorithm 6 NODE(k, v, left, right, parent) 1: w new node 2: w.key k 3: w.value v 4: w.left left 5: w.right right 6: w.parent parent 7: w.min k 8: w.max k 9: return w Note that this version of the BST data structure must maintain the invariant that the data members w. min and w. max of every node whold the smallest and largest keys in the subtree rooted at w. Hence, both the insertion and removal operations must be properly adapted. Complete the implementation of updatelnfo in Algorithm 8, given below, which would be useful for the adaptation of the the insertion and removal operation. The method takes as input a node w. It has the precondition that all the descendant nodes of w, possibly excluding witself, satisfy the invariant. It has the postcondition that all the ancestors of satisfy the invariant. (Match each missing statement # on the left with the proper operation on the right.) Algorithm 8 UPDATEINFO(w) 1: while w NULL do 2: if w.left 3: 4: 5: 6: 7: 8: 9: 10: Statement 3 Statement 5 Statement 7 Statement 9 Statement 10 else = if w.right else NULL then - NULL then [Choose] [Choose w.min