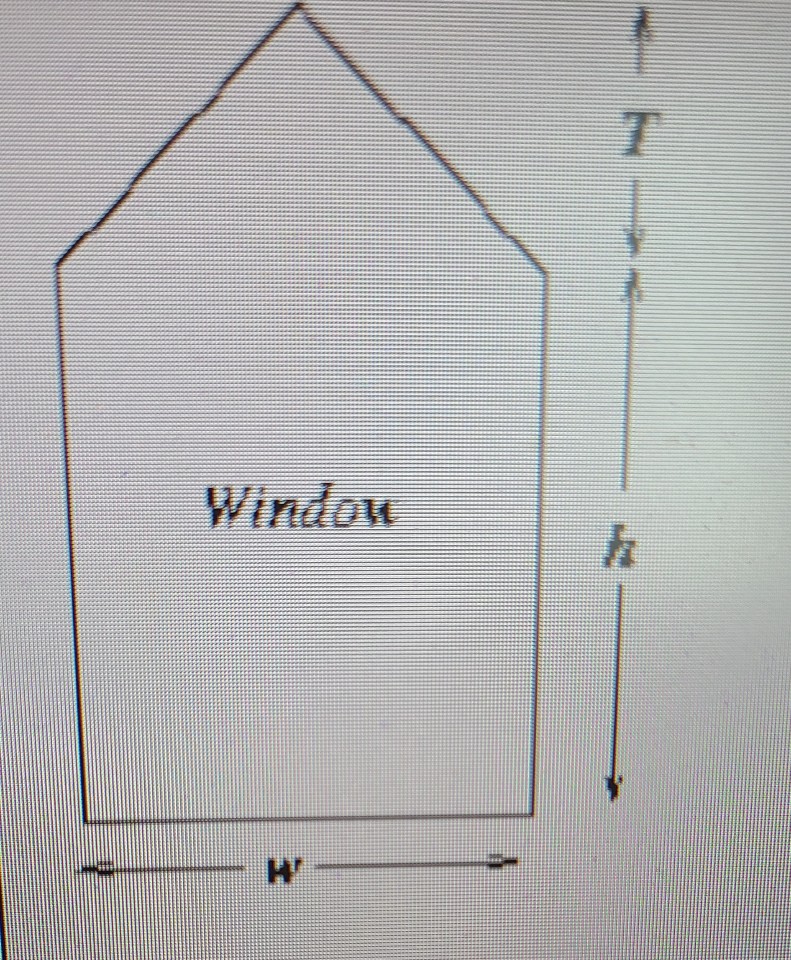
Question: Consider a window the shape of which is a rectangle of height h surmounted by a triangle having a height T that is 0.6 times

Consider a window the shape of which is a rectangle of height h surmounted by a triangle having a height T that is 0.6 times the width w of the rectangle (as shown in the figure below).

If the cross-sectional area isA, determine the dimensions of the window which minimize the perimeter.

h =

w =

P.S. I found the answer for W. W = sqrt(2*A/(1-0.6+2*sqrt(0.6*0.6+1/4))), I need the answer for H in this format

Consider a window the shape of which is a rectangle of height

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Consider a window the shape of which is a rectangle of height h surmounted a triangle having a height T that is 1 times the width w of the rectangle (as shown in the figure below). If the...

Consider a window the shape of which is a rectangle of height h surmounted by a triangle having a height T that is 0.3 times the width w of the rectangle (as shown in the figure below). Window If the...

Consider a window the shape of which is a rectangle of height h surmounted by a triangle having a height T that is 0.3 times the width w of the rectangle (as shown in the figure below). If the cross...

Need this lab done for computer science as soon as possible. I will include all the starter files. Playing with Buttons and Drawing In this lab you will create a GUI that will calculate the area and...

Consider a window the shape of which.is a rectangle of height h surmounted by a triangle having a height T that is 0.3 times the width w of the rectangle (as shown in the figure below). My Window If...

1. Define the class Shape with two private data members width and height (both double). The Shape class should have a default constructor as well as constructor with parameters. The class should have...

C++ Email solution to rolphmunz@yahoo.com Will pay $50 with paypal. 1. Define the class Shape with two private data members width and height (both double). The Shape class should have a default...

Java please Description Write a program that reads a list of graphics primitives from a text file and draws them in a window. This assignment creates a set of Java classes in a very primitive...

The work to be done is in the photo provided above ^ Here is the code she provided already: /* JH: Compile with g++ drawing.cpp -lcurses more about the NCURSES libary:...

Gemma is a 32 year old female who has no kids, needs regular dental check-ups and wears glasses at times and has contacts. Which policy is the best for her? Medical premium per month Dental premium...

Why do camera flashes make your eyes turn red?

Recharge ur Answer A proforma balance sheet indicates that total assets will increase by $ 3 0 0 , 0 0 0 . If a debt - equity ratio of 0 . 5 is maintained then debt must increase by: $ 1 0 0 , 0 0 0...

Fill in the missing amounts. Cheyenne Corp. Oriole Company $106,000 $ Sales revenue Sales returns and allowances Net sales Cost of goods sold 6,600 122,000 100,000 65,000 Gross profit 45.140...