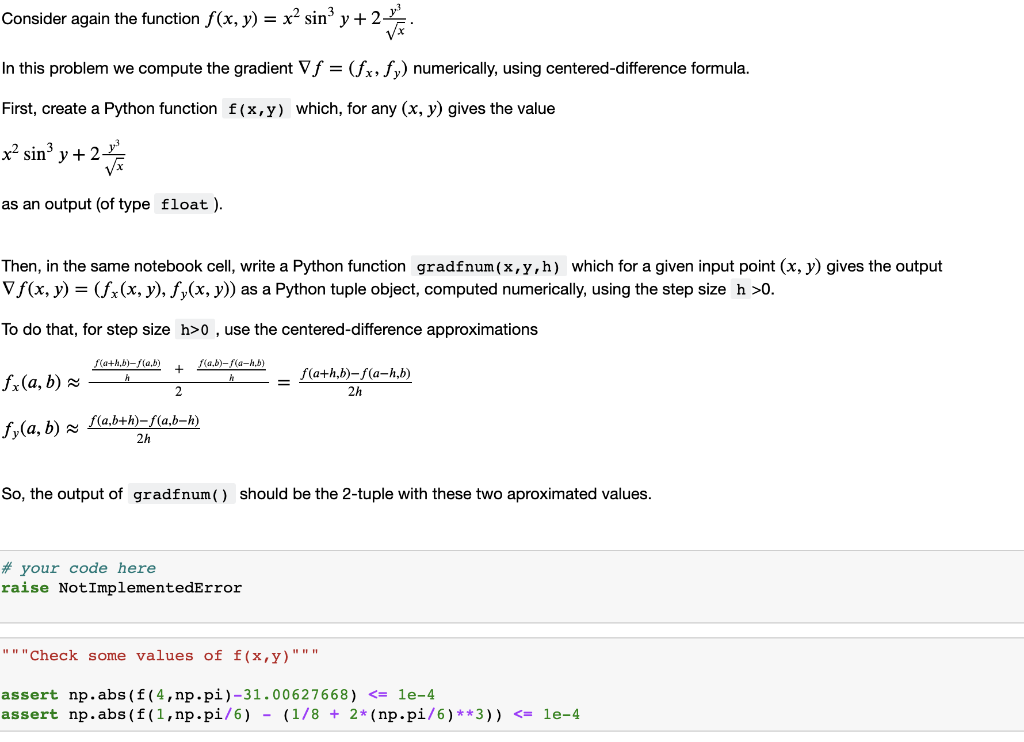
Consider again the function f(x, y) = x? sin y+2 In this problem we compute the gradient V f = (fx, fy) numerically, using centered-difference formula. First, create a Python function f(x,y) which, for any (x, y) gives the value x? siny+2 as an output (of type float). Then, in the same notebook cell, write a Python function gradfnum(x,y,h) which for a given input point (x, y) gives the output V f(x, y) = (fx(x, y), fy(x, y)) as a Python tuple object, computed numerically, using the step size h >0. To do that, for step size h>0 , use the centered-difference approximations f(a+h.b)-f(a,b) f(a,b)-f(a-h.b) fx(a,b) f(a+h,b)-f(a-h,b) 2h 2 fy(a,b) f(a,b+h)-f(a,b-h) 2h So, the output of gradfnum() should be the 2-tuple with these two aproximated values. # your code here raise NotImplementedError """Check some values of f(x,y)" assert np.abs(f(4, np.pi)-31.00627668)