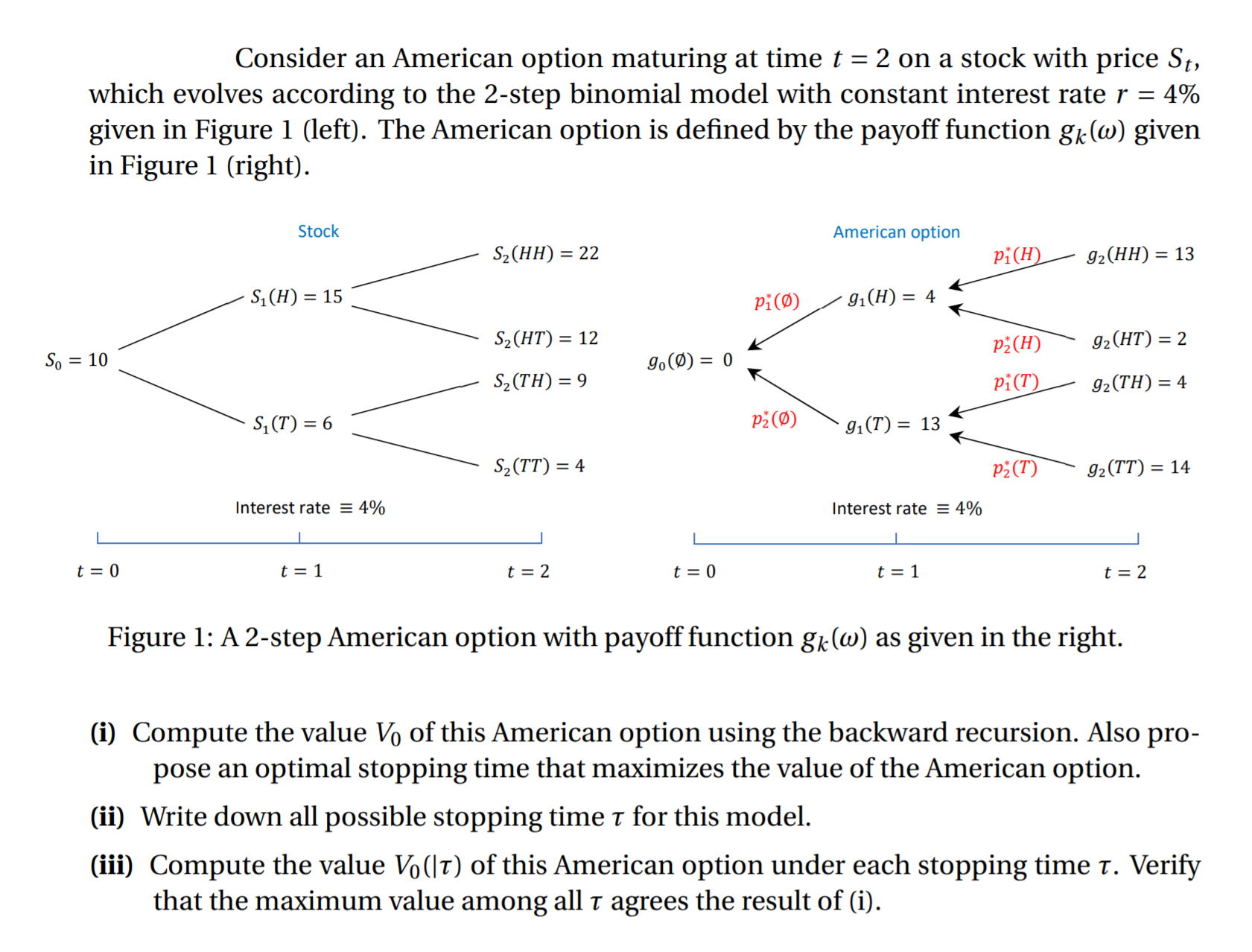
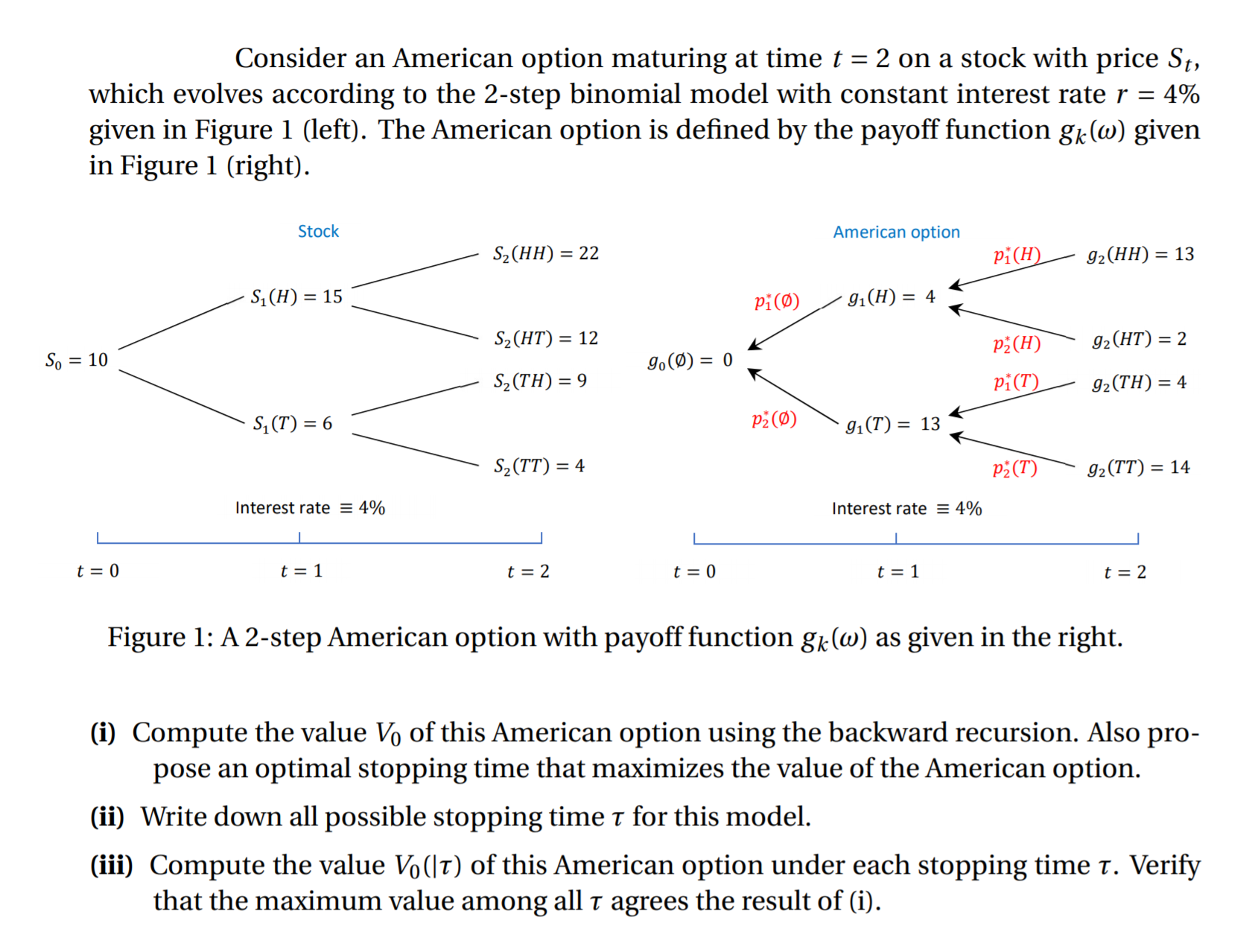
Consider an American option maturing at time t = 2 on a stock with price 8,, which evolves according to the 2step binomial model with constant interest rate r = 4% given in Figure 1 (left). The American option is dened by the payoff function gk(w) given in Figure 1 (right). Stock 52041;) = 22 31(H) = 15 32 (HT) = 12 52 (TH) = 9 50:10/ \ 510') = 6 /\/\ 32m") = 4 Interest rate E 4% I | I t=0 t=1 t=2 American option y/ 920%): 13 101(9) 91(H) = 4 \ g (0) - 0 / 175(H) 92(HT) =2 0 _ \ y gz(TH)=4 115(0) 910') = 13 '% 91m"): 14 Interest rate E 4% | | | t=0 t=1 t=2 Figure 1: A 2step American option with payoff function gkuo) as given in the right. (i) Compute the value V0 of this American option using the backward recursion. Also pro- pose an optimal stopping time that maximizes the value of the American option. (ii) Write down all possible stopping time I for this model. (iii) Compute the value V0(|r) of this American option under each stopping time 1'. Verify that the maximum value among all r agrees the result of (i)