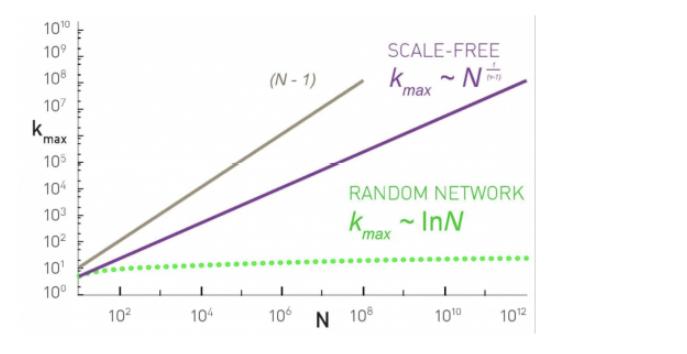
Consider an Erdos-Renyi random network with parameters N and p, and with a simplified Poisson degree distribution P(k; = k) = C.ek where C and A are constants with C, A > 0. Use kmin to represent the smallest degree. (a) Find an analytical solution for C, the normalization parameter, as a function of kmin and X. (b) kmax is the value of k such that P(k> kmax) < 1/N in expectation. That is, in expectation, there are less than 1 node with degree greater than kmaz, which is to say there are no nodes with degree greater than kmax in expectation. Use this information to approximate kmax as a function of N. Use your solution from (a) to substitute in for C. Go to Settings to 1010 10 108 107 k max 105 104 10 10 10 10 10 104 (N-1) 10 N SCALE-FREE ~N k 108 RANDOM NETWORK k max max InN 1010 102