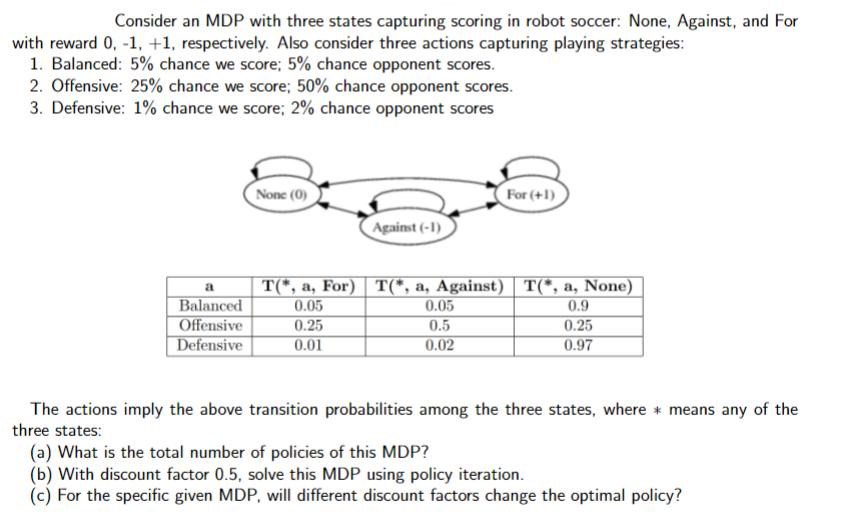
Consider an MDP with three states capturing scoring in robot soccer: None, Against, and For with reward 0, -1, +1, respectively. Also consider three actions capturing playing strategies: 1. Balanced: 5% chance we score; 5% chance opponent scores. 2. Offensive: 25% chance we score; 50% chance opponent scores. 3. Defensive: 1% chance we score; 2% chance opponent scores a Balanced Offensive Defensive None (0) Against (-1) 0.25 0.01 T(*, a, For) T(*, a, Against) | T(*, a, None) 0.05 0.9 For (+1) 0.05 0.5 0.02 0.25 0.97 The actions imply the above transition probabilities among the three states, where means any of the three states: (a) What is the total number of policies of this MDP? (b) With discount factor 0.5, solve this MDP using policy iteration. (c) For the specific given MDP, will different discount factors change the optimal policy?