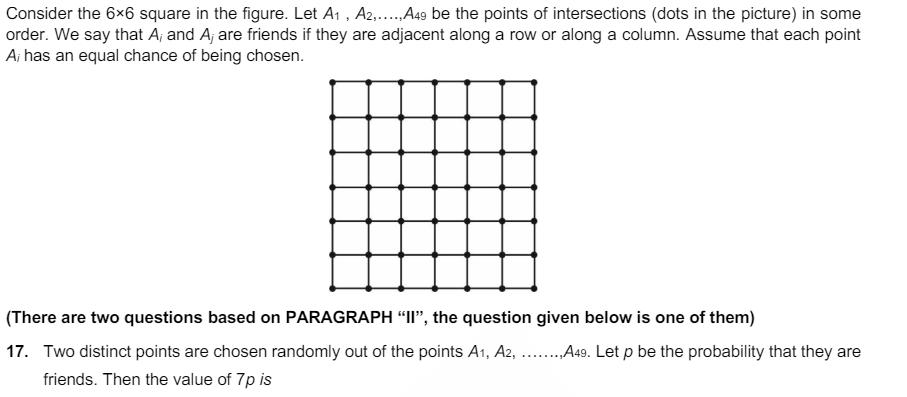
Consider an obtuse angled triangle ABC in which the difference between the largest and the smallest angle is 2 and whose sides are in arithmetic progression. Suppose that the vertices of this triangle lie on a circle of radius 1. (There are two questions based on PARAGRAPH "I", the question given below is one of them) 14. Let a be the area of the triangle ABC. Then the value of (64a)2 is Consider an obtuse angled triangle ABC in which the difference between the largest and the smallest angle is and whose sides are in arithmetic progression. Suppose that the vertices of this triangle lie 2 on a circle of radius 1. (There are two questions based on PARAGRAPH "I", the question given below is one of them) 15. Then the inradius of the triangle ABC is Consider the 66 square in the figure. Let A1, A2,...,A49 be the points of intersections (dots in the picture) in some order. We say that A, and A, are friends if they are adjacent along a row or along a column. Assume that each point A; has an equal chance of being chosen. si 'S (There are two questions based on PARAGRAPH "II", the question given below is one of them) 16. Let p be the probability that a randomly chosen point has i many friends, i = 0, 1, 2, 3, 4. Let X be a random variable such that for i = 0,1, 2, 3, 4, the probability P (X = i) = p. Then the value of 7E(X) is Consider the 66 square in the figure. Let A1, A2,.....A49 be the points of intersections (dots in the picture) in some order. We say that A, and A, are friends if they are adjacent along a row or along a column. Assume that each point A; has an equal chance of being chosen. (There are two questions based on PARAGRAPH "II", the question given below is one of them) 17. Two distinct points are chosen randomly out of the points A1, A2, A49. Let p be the probability that they are friends. Then the value of 7p is