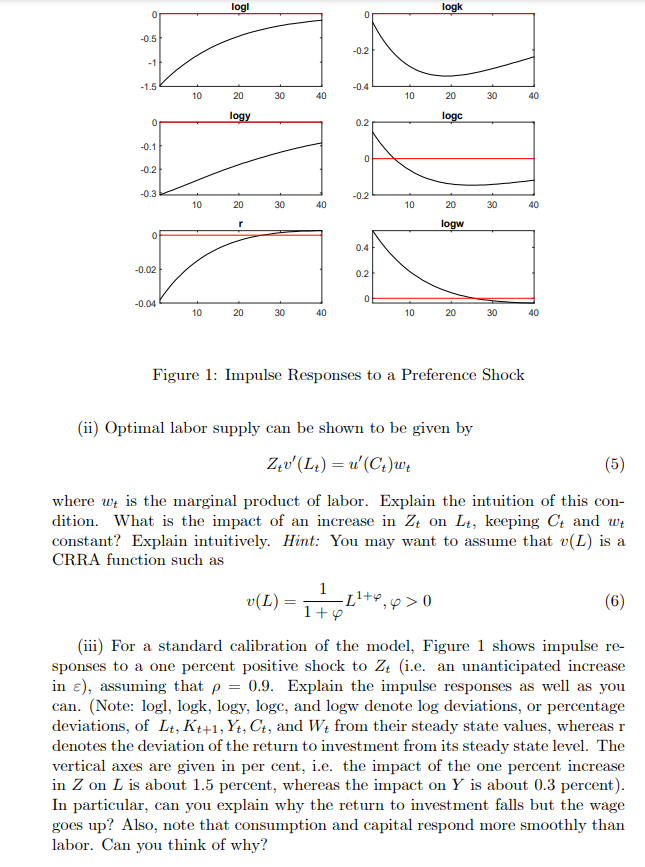
Consider an optimal growth model in which output is produced with capital and labor: a = AKfLi'\" (1) where L: denotes hours worked, A 2) I} is a constant, and the other symbols have usual meanings. IGapital accumulation has the usual form: Kt+1 = [1 5)Kt+YtCt [2} and the representative household has preferences 52 t[(0tl Zt'viLtl] t= This specication differs from the usual one in that Z: is a random process (Le. a shock to preferences). For simplicity, we will assume that it follows the 1113(1) process: 105 Z: = 9103 Ztl + E: [3) where I pl { l and at is a white noise with mean zero and standard deviation :35. (i) One can show that, in this case, the Euler condition of this problem is the usual one: \"'(Ctl = Etu'{Ct+1)Rt+1 [4} where Rt+1 is the investment return realized at t + 1. Explain the intuition for this condition. Find an explicit expression for Rt+1 and briey explain its meaning. Figure 1: Impulse Responses to a Reference Shock (ii) Optimal labor supply can be shown to be given by 3:9!{Lt} = u"{C,}wt [5} where He is the marginal product of labor. Explain the intuition of this con dition. What is the impact of an increase in E; on Lt, keeping C: and tot constant? Explain intuitively. Hint: You may want to assume that a{L} is a CRRA function such as 1 UiL} = le+P, [P 33' {6'} {iii} Fer a standard calibration of the model, Figure 1 shows impulse re sponses to a one percent positive shock to E; {i.e. an unanticipated increase in E], aSSuming that p = [1.9. Explain the impulse reapenaea as well as you can. (Note: logl, logk, logy, logo, and logw denote log deviations, or percentage deviations, of Lt, If,\" , Kg, 0,, and Wt from their steady state values, whereas r denotes the deviation of the return to investment from its steady state level. The vertical axes are given in per cent, i.e. the impact of the one percent increase in Z on L is about 1.5 percent, whereas the impact on Y is about [1.3 percent}. In particular, can you explain why the return to investment falls but the wage goes up? Also, note that cenSuniption and capital respond more srnoothly than labor. Can you think of why