Consider CONNECTED-COMPONENTS algorithm. Let G = (V, E) be the input graph, n = |V|, m = |E|, k = the # of connected components of G.

CONNECTED-COMPONENTS (G) algorithm

for each vertex {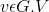

MAKE-SET(v) }

for each edge (u,v) {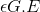

if FIND_SET(u) != FIND-SET(v){

UNION(u,v) }

}

a. Determine and express the exact # of times Union is called in terms of n and k.

b. Presume that Make-Set, Find-Set, Union are implemented by forests with rank and path compression. Analyze the runtime efficiency of CONNECTED-COMPONENTS and express it in O( ) notation; use the result of question (a) and Theorem 21.14 on page 581.

c. Modify CONNECTED-COMPONENTS so that it will also compute the set of edges in a spanning forest of G. A spanning forest of G is a set of spanning trees of the connected components of G.