Question: Consider fn(x) = nx (1 -x) for x E [0, 1]. (a) Find f(x) = lim fr(x). (b) Does fn -> f uniformly on [0,

Consider fn(x) = nx" (1 -x) for x E [0, 1].

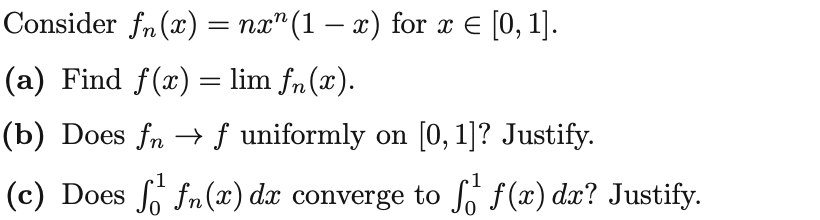
Consider fn(x) = nx" (1 -x) for x E [0, 1]. (a) Find f(x) = lim fr(x). (b) Does fn -> f uniformly on [0, 1]? Justify. (c) Does for fn(x) dx converge to f f(x) dx? Justify

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

MATH 2500: TAKE HOME 02 (30 points.) NAME: DUE: Wednesday, June 3rd by 8 AM. DIRECTIONS: To receive full credit, make sure your work is neat and complete. 1. Let f (x) = x + sin(x) 1. (a) Explain why...

Use the given graph of the function f to answer parts (a)(o). L (-3,0) -5 (0, 3) (-5,-2) YA I (2,4) 1 (4,3) I 5 (6, 0) (-6,-3) (a) Find f (0) and f(-6). (b) Find f (6) and f(11). (c) Is f(3) positive...

need help with practice questions MCV4U Practice Answer (or Solution) Practice Questions 1. Consider the function f(x) defined by the following graph: 2 1-4 -3 -2 -1 2 Find: a) lim f(x) b) lim f(x)...

3a. " Let fn : [0, 1] - R be defined by fn (x) = n2x (1 - x)". Is is true that lim n-co Jo fn (x) dx = lim fn (x) dx n-00 Hint: Show that So fn(x) dx = n2 (n+1)(n+2) and fn - f = 0 pointwise. 3b. Let...

Math 125 A: Homework 5 Due Thursday, November 9 1. For n = 1, 2, let fn : E R and suppose that fn f uniformly for some function f . Show that if each fn is bounded, then f is bounded. 2. Let {fn } be...

need help with my worksheetsss MCV4U Unit 2 - Activity 2 The Derivatives of Polynomial Functions We have seen that derivatives of functions are of practical use because they represent instantaneous...

9) A function is uniformly continuous on a set I C R if a) for some e > 0 we can find a 6 > 0 such that if x, y 1 and 6, then I b) for any e > 0 we can find a > 0 such that if x, y e I and I x y 5,...

Section 8.5 Reading Assignment: Integration of Rational Functions by Partial Fractions Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read...

all the info has been attached f ( x ) - L / > E Question 4, 2.7 e O Points: 0 of 1 If ( x ) - L - 6 x - a 8 te the steps for proving that lim f(x) = L. x-a f (x ) - L 0, assume and use the...

03 DIFFERENTIATION HOMEWORK 14 Date: Definition of Derivative I A. Use the definition of derivative to find f'(x) for the following functions. Example 1. f(x) = 3x2 + x f ( x ) = 2 1 - X f'(x) = lim...

in 1919, Tesco has grown from a market-stall in the East End of London into the largest supermarket in the UK by market share, and one of the largest glob- ally in just under a century. In 2018-19,...

Calculate the annual cost in years 1 through 9 of the following series of disbursements. Use an interest rate of 10% peryear. Year Disbursement, S Year Disbursement, $ 5000 5500 6000 6500 7000 7500...

1. Products can be made failure proof.

A system consists o f four subassemblies connected i n series. The individual subassembly reliabilities are a s follows: Subassembly A = 0 . 9 8 Subassembly B = 0 . 8 5 Subassembly C = 0 . 9 0...

Identify two rivals and two complementors for each of the following companies. Rivals could include incumbent competitors, substitutes or potential new entrants. (a) Toyota (b) Microsoft (c) Lenovo...

Examine the corporate Web sites of the following companies and determine if the strategies pursued by these firms were emergent, deliberate, or both emergent and deliberate. Justify your answer with...

Suppose you have to evaluate microfinance ventures. One of the proposals is for opening a hairdressers shop in Guatemala City. The proposal argues that there must be significant demand for...