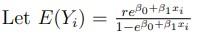
Consider independent random variables Y1,,Yn following the negative binomial distribution with the following probability distribution: f(yi;)=(yi+r1r1)r(1)y,yi=0,1, for 01 (a) Let E(Yi)=1e++1xir2e0+i1xi for all i=1,,n. Is this a GLM? Give reasons for your answer. (b) Find the score statistics U and the Fisher information matrix, J=Var(U). Verify that E(U)=0. Let E(Yi)=1e0+1xire0+1xi Consider independent random variables Y1,,Yn following the negative binomial distribution with the following probability distribution: f(yi;)=(yi+r1r1)r(1)y,yi=0,1, for 01 (a) Let E(Yi)=1e++1xir2e0+i1xi for all i=1,,n. Is this a GLM? Give reasons for your answer. (b) Find the score statistics U and the Fisher information matrix, J=Var(U). Verify that E(U)=0. Let E(Yi)=1e0+1xire0+1xi