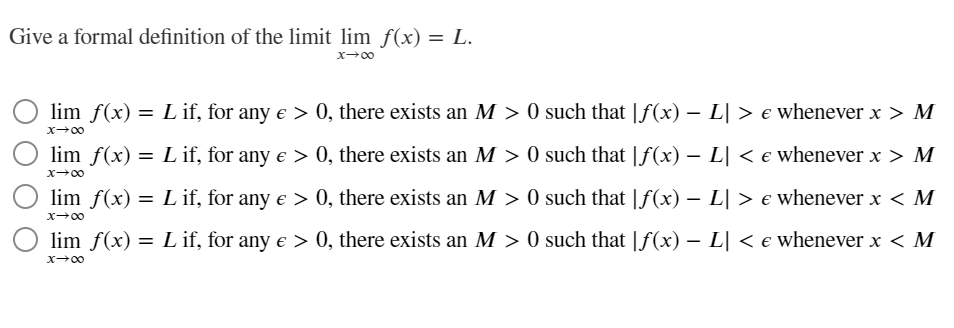
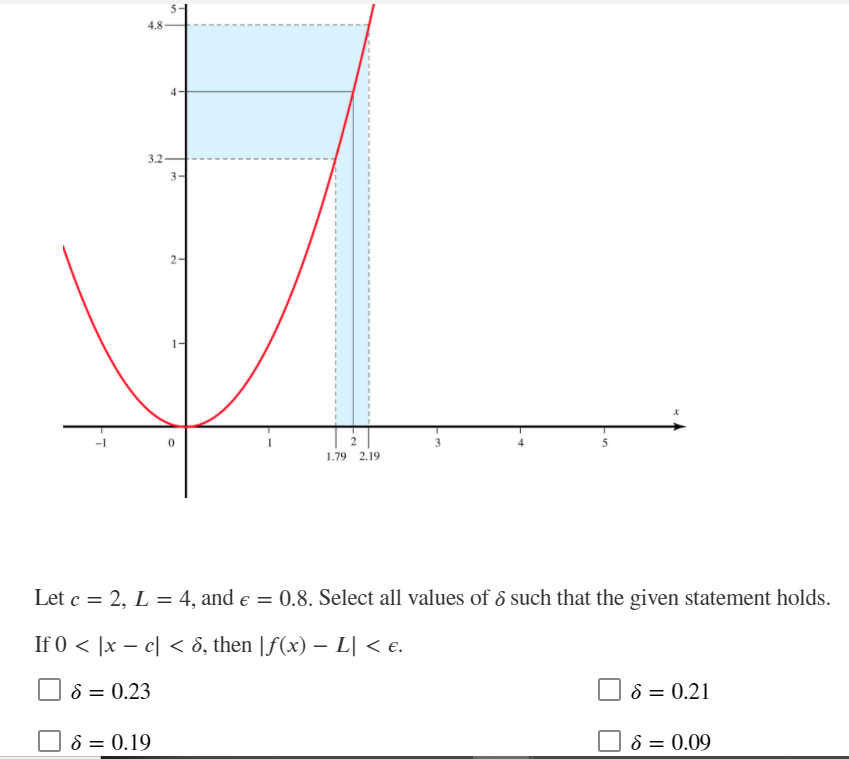
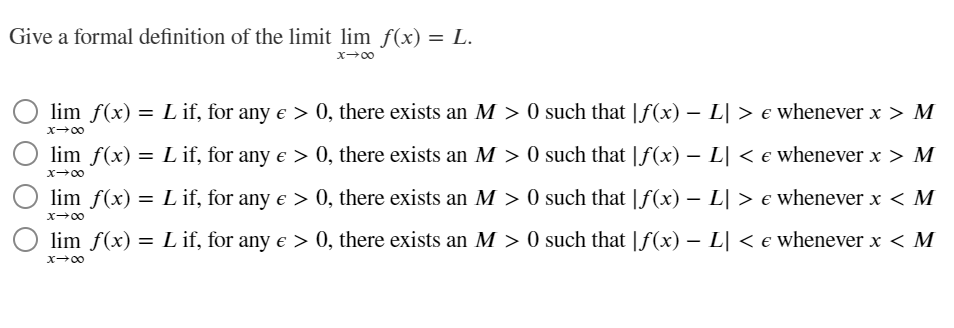
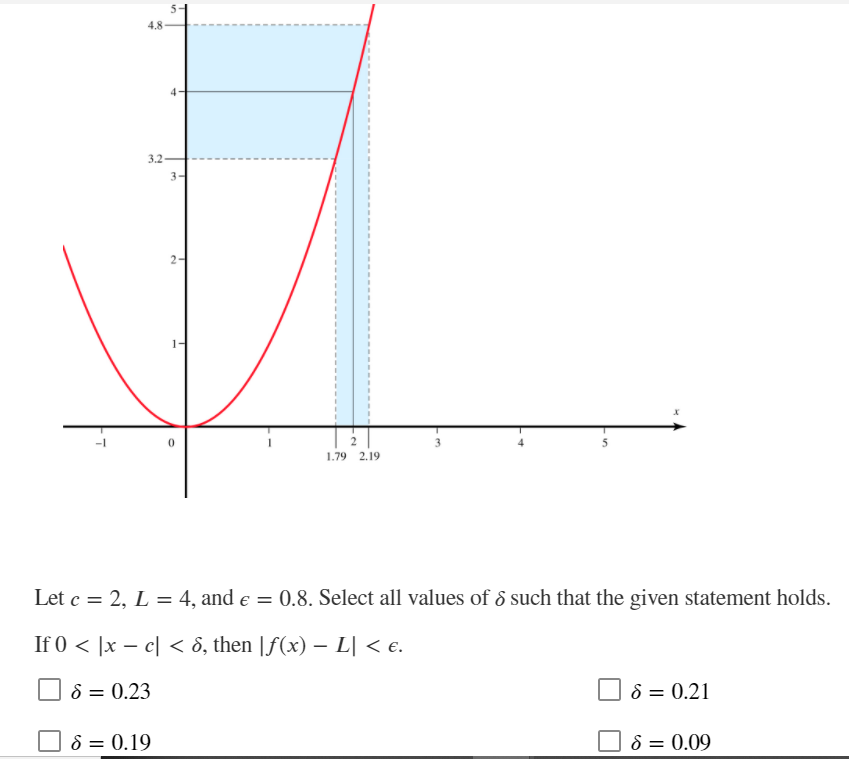
Consider limx_,5 x), where f(x) = 13): + 4. Find a maximum value of 5 such that: |f(x) 69| 0, there exists an M > 0 such that If(x) - L| > e whenever x > M X-+00 O lim f(x) = L if, for any e > 0, there exists an M > 0 such that If(x) - L| M X-+00 O lim f(x) = L if, for any e > 0, there exists an M > 0 such that If(x) - L| > e whenever x 0, there exists an M > 0 such that If(x) - L| 0, we need o such that if 0