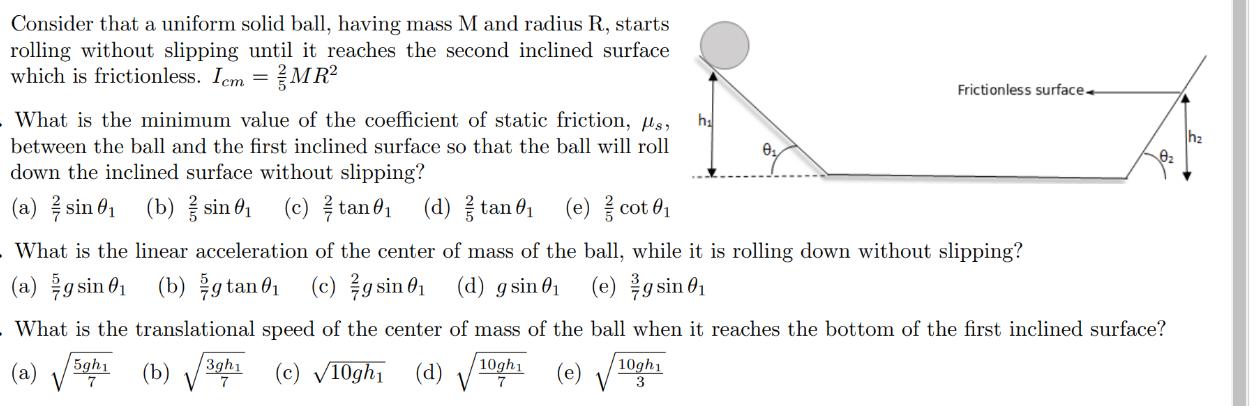
Consider that a uniform solid ball, having mass M and radius R, starts rolling without slipping until it reaches the second inclined surface which is frictionless. Icm = MR What is the minimum value of the coefficient of static friction, s, between the ball and the first inclined surface so that the ball will roll down the inclined surface without slipping? (a) sin 0 (b) sin 0 (c)tan 0 (d) / tan 0 (e) //cot 0 5gh1 7 h What is the linear acceleration of the center of mass of the ball, while it is rolling down without slipping? (a)gsin 0 (b) gtan 01 (c) g sin 0 (d) g sin 0 (e) g sin 01 10gh1 0 . What is the translational speed of the center of mass of the ball when it reaches the bottom of the first inclined surface? 3gh1 (a) (b) (c) 10gh (d)10h (e) V V 3 Frictionless surface-