Question: Consider the 1-2 tiling problem. You are given a 1n area that you need to tile with some combination of 1 1 and 1 2
Consider the 1-2 tiling problem. You are given a 1n area that you need to tile with some combination of 1 1 and 1 2 tiles, and you need to determine how many ways there are to tile this area
For example, there are 3 ways to tile a 1 3 area:
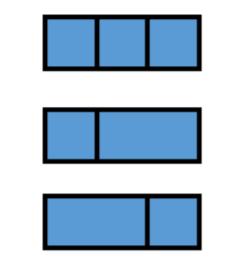
Give pseudocode for a divide-and-conquer algorithm for this problem. There is an O(n) solution, though a less efficient solution may be acceptable, as long as it is sub-exponential
Hint: you will probably want to consider odd and even n separately. One useful observation is that there are only 3 ways to cover a tile in the middle of the area: a 1 1 tile, a 1 2 tile that extends to the left, and a 1 2 tile that extends to the right. Also, when dividing up your problem, dont forget about the possibility of a 12 block crossing the boundary between two subproblems.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


