Consider the (7,4) block error correcting code shown below and table shown below, with generator polynomial P(X)=X^3+X^2+1. A destination node receives bits 1011101. Compute the syndrome with the polynomial division and determine the original transmitted data bits and the original message.

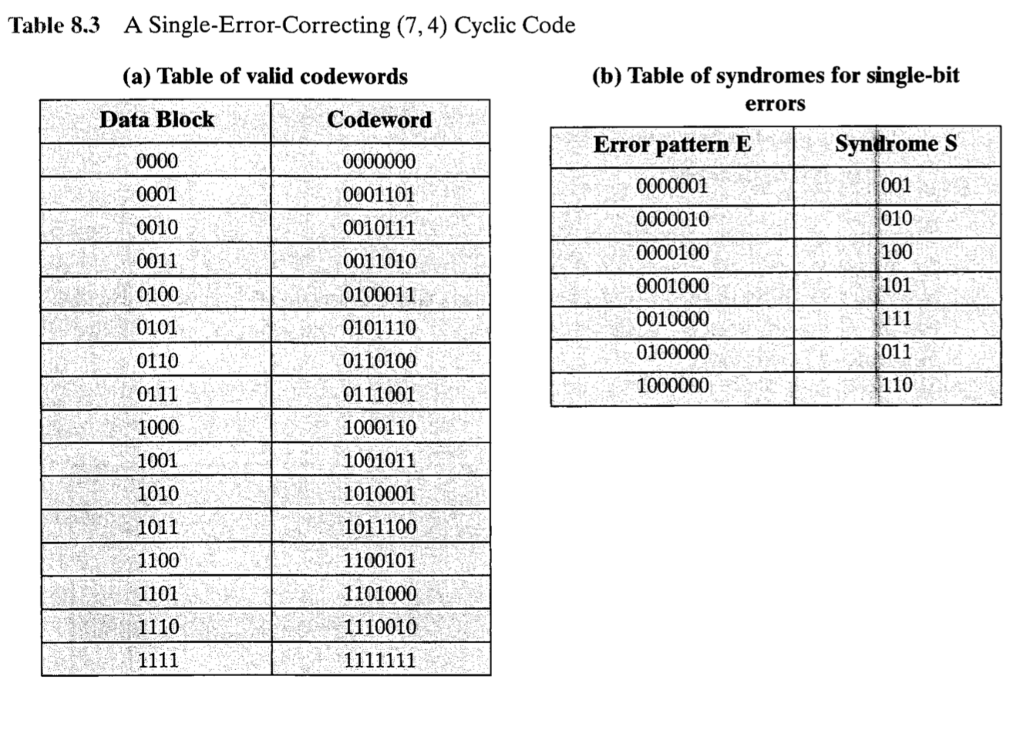
Example 8.85 Consider a (7, 4) code with the generator polynomia PX)XX2+1. We have 723 1, so this code is capable of correcting all single-bit errors. Table 8.3a ists all of the valid codewords; note that dmin is 3, confirming that this is a single-error-correcting code. For example, for the data block 1010, we have D(X,-X' + X and Xn-kD(x) = x xa. Dividing as in Equation (8.4): x3+x21 x3 + x2 x3+x2+ Then, using Equation (8.3), we have T(x) X X4 +I, which is the code vord 1010001 For error correction, we need to construct the syndrome table shown in Table 83b. For example, for an error pattern of 1000000, E(X) X6. Using the last line of Eqlation (8.6), we calculate: Example 8.85 Consider a (7, 4) code with the generator polynomia PX)XX2+1. We have 723 1, so this code is capable of correcting all single-bit errors. Table 8.3a ists all of the valid codewords; note that dmin is 3, confirming that this is a single-error-correcting code. For example, for the data block 1010, we have D(X,-X' + X and Xn-kD(x) = x xa. Dividing as in Equation (8.4): x3+x21 x3 + x2 x3+x2+ Then, using Equation (8.3), we have T(x) X X4 +I, which is the code vord 1010001 For error correction, we need to construct the syndrome table shown in Table 83b. For example, for an error pattern of 1000000, E(X) X6. Using the last line of Eqlation (8.6), we calculate