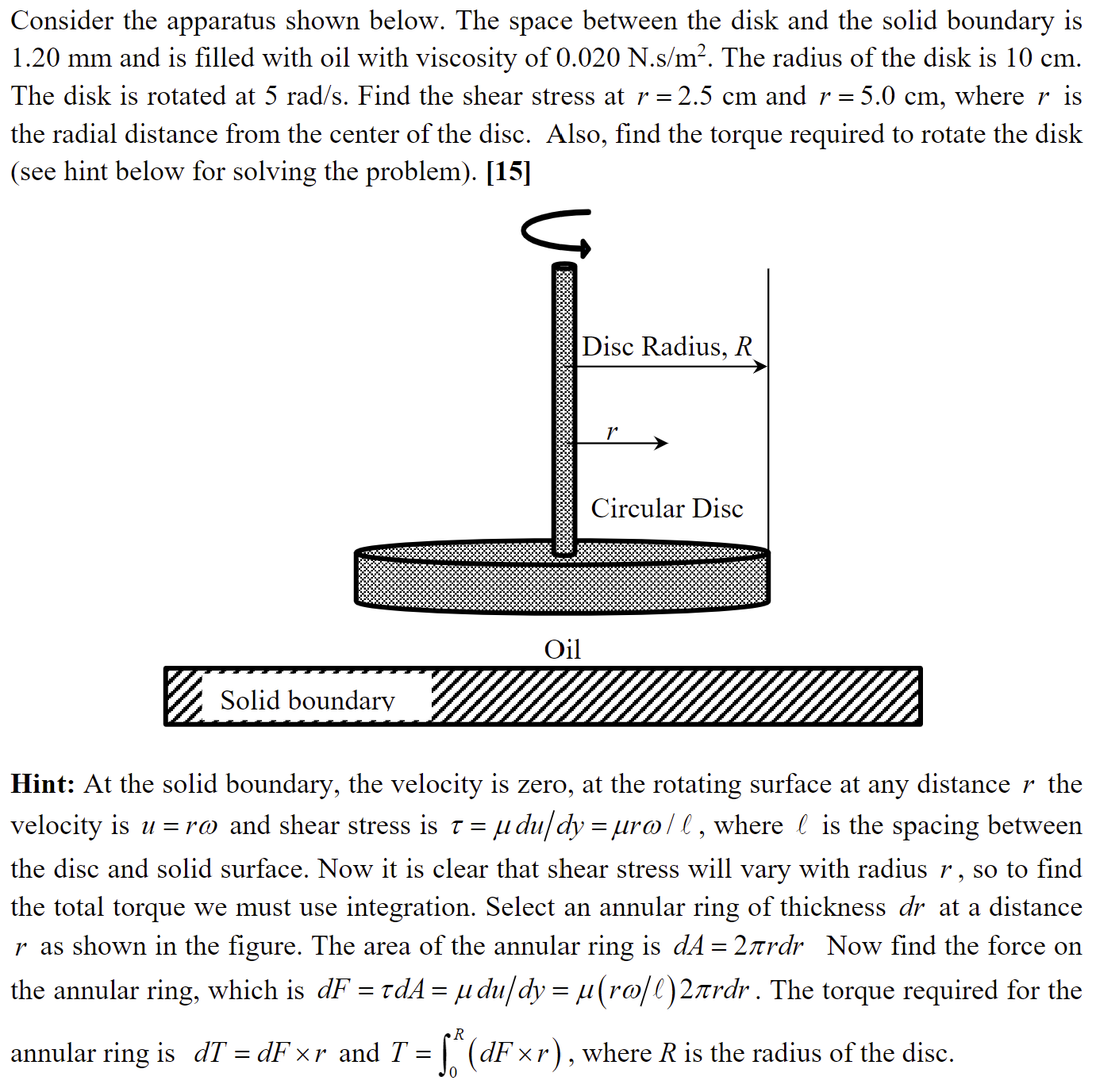
Consider the apparatus shown below. The space between the disk and the solid boundary is

$1\mathrm{.}20mm$ and is filled with oil with viscosity of $0\mathrm{.}020N.\frac{s}{m^2}.$ The radius of the disk is $10cm.$

The disk is rotated at $5ra\frac{d}{s}.$ Find the shear stress at $r=2\mathrm{.}5cm$ and $r=5\mathrm{.}0cm,$ where $r$ is

the radial distance from the center of the disc. Also, find the torque required to rotate the disk

$($see hint below for solving the problem$).[15]$

Hint: At the solid boundary, the velocity is zero, at the rotating surface at any distance $r$ the

velocity is $u=r$ and shear stress is $=d\frac{u}{d}y=r\frac{}{l},$ where $l$ is the spacing between

the disc and solid surface. Now it is clear that shear stress will vary with radius $r,$ so to find

the total torque we must use integration. Select an annular ring of thickness $dr$ at a distance

$r$ as shown in the figure. The area of the annular ring is $dA=2rdr$ Now find the force on

the annular ring, which is $dF=dA=d\frac{u}{d}y=(r\frac{}{l})2rdr.$ The torque required for the

annular ring is $dT=dFr$ and $T={\displaystyle \underset{0}{\overset{R}{}}}(dFr),$ where $R$ is the radius of the disc.