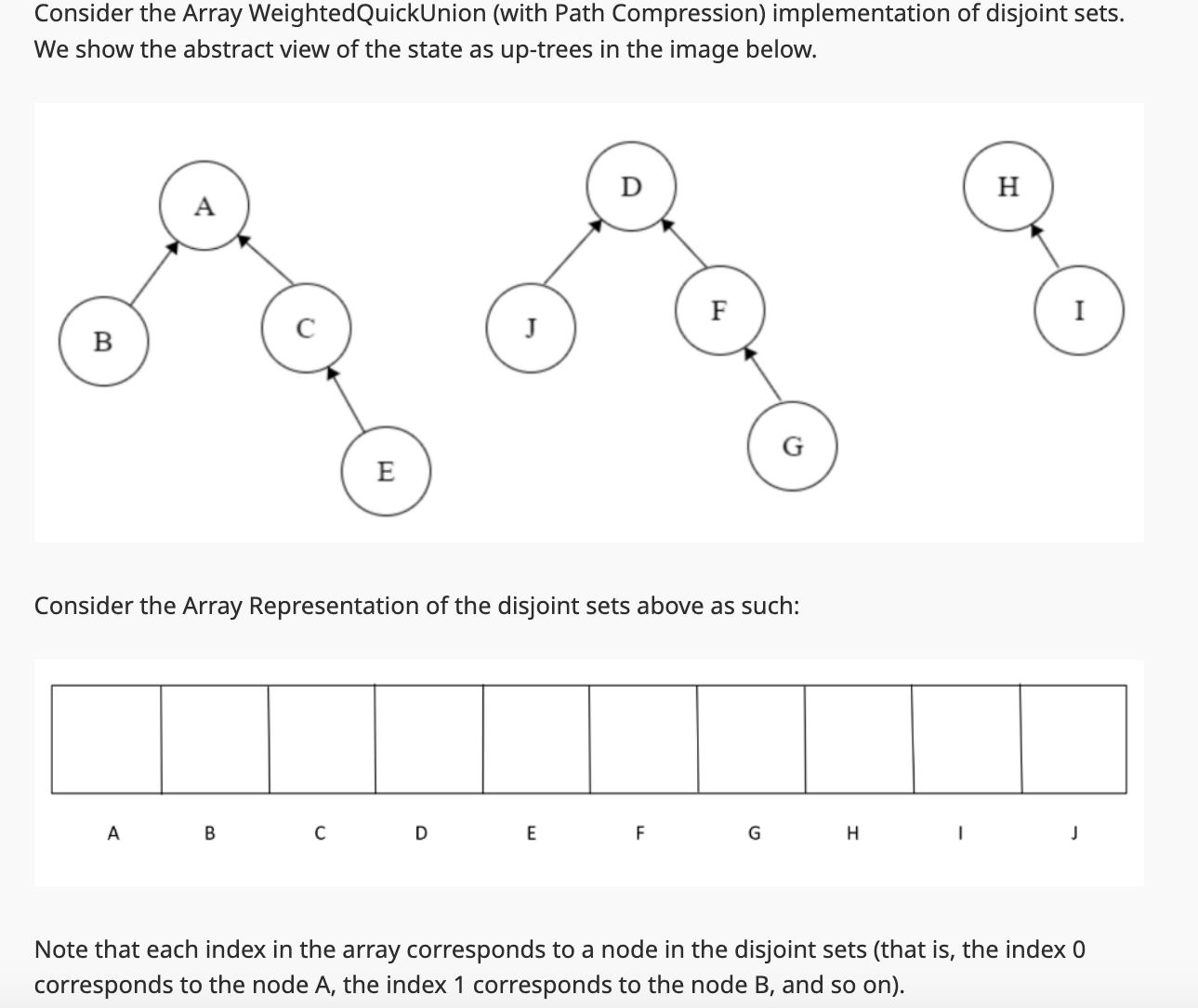
Consider the Array WeightedQuickUnion (with Path Compression) implementation of disjoint sets. We show the abstract view of the state as up-trees in the image below. B A C A B E J D D Consider the Array Representation of the disjoint sets above as such: E F F G H H I Note that each index in the array corresponds to a node in the disjoint sets (that is, the index 0 corresponds to the node A, the index 1 corresponds to the node B, and so on). Q5.1 Array Representation 2 Points Fill in the array representation for the disjoint sets above. Note that you should write the index as a number corresponding to the node since arrays are indexed as such. The array picture above shows the mapping from which value goes to which index. Enter your answer below as comma-separated values in the order as the values appear in the array above. Save Answer Q5.2 Calling Operations 2 Points Now provide the array representation for the disjoint sets after calling union (G, H) on the disjoint sets above. Enter your answer below as comma-separated values in the order as the values appear in the array above. Save Answer