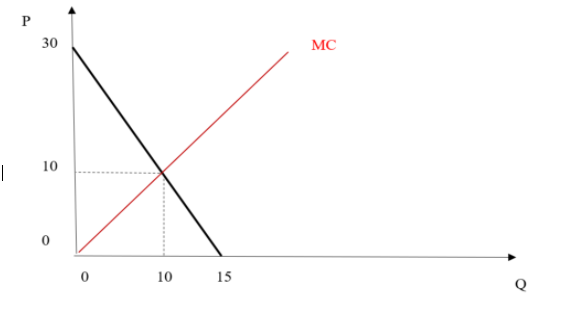
Consider the case where a monopolist's inverse demand function equals P = 30 -2Q, and the firm's total costs are given by C(Q) = (1/2)Q2, which results in a marginal cost equal to Q. The following illustration depicts the output that maximizes total surplus. This output is economically efficient.

Total Surplus is maximized when the firm produces 10 units. Total surplus equals $150 when output equals 10.The total amount consumers are willing to pay (WTP) for 10 units of the good equals the area under the demand curve.WTP (10) = 10 x 10 + (1/2) (30 - 10) x 10 = 100 + 100 = $200

The total variable cost of producing 10 units equals the area underneath the marginal-cost curve, which equals (1/2) x 10 x 10 = $50

The different between WTP and variable cost equals total surplus. WTP - TVC = $200 - $50 = $150.The single-price monopolist maximizes profit by producing 6 units and setting price equals to $18. The monopolist's profit equals $90. The single-price monopolist only captures 60 percent of the total surplus available in this market.