Question: Consider the data generation process for observation pair (a, b) as follows: - a is the outcome of an independent six-faced (possibly loaded) dice-roll. That
Consider the data generation process for observation pair (a, b) as follows:
- a is the outcome of an independent six-faced (possibly loaded) dice-roll. That is, chance of rolling face '1' is p1, rolling face '2' is p2, etc., with a total of six distinct possibilities.
- Given the outcome a, b is drawn independently from a density distributed as 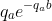 (where qa > 0).
(where qa > 0).
(i) List all the parameters of this process. We shall denote the collection of all the parameters as the variable (the parameter vector).
(ii) Suppose we run this process n times independently, and get the sequence: (a1, b1),(a2, b2), . . . ,(an, bn). What is the likelihood that this sequence was generated by a specific setting of the parameter vector ?
(iii) What is the most likely setting of the parameter vector given the complete observation sequence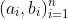 ? that is, find the Maximum Likelihood Estimate of given the observations.
? that is, find the Maximum Likelihood Estimate of given the observations.
(iv) What is the probability of the partial (incomplete) observation b1, b2, . . . , bn given a specific setting of the parameter vector ?
(v) Derive the Expectation Maximization (EM) algirthm to estimate of the parameters given the incomplete observation sequence 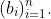
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


