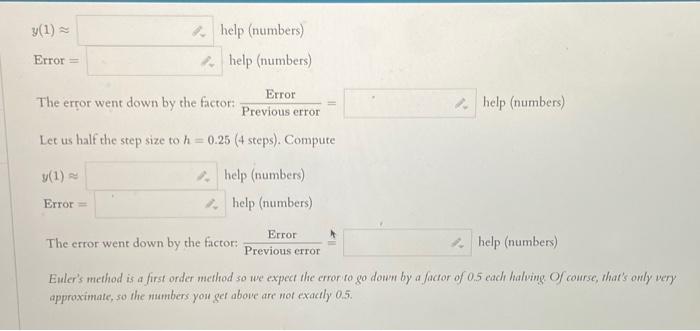
Consider the differential equation = 2y with initial condition y(0) = 0.7. The actual solution is y(1) = help (numbers) We wish to analyze what happens to the error when estimating y(1) via Euler's method. Start with step size h= 1 (1 step). Compute Error = Note: Remember that the error is the absolute value! Let us half the step size to h = 0.5 (2 steps). Compute y(1) help (numbers) help (numbers) Error= help (numbers) help (numbers) Error The error went down by the factor: Previous error Let us half the step size to h= 0.25 (4 steps). Compute help (numbers) y(1) Error= help (numbers) help (numbers) Error The error went down by the factor: Previous error Let us half the step size to h= 0.25 (4 steps). Compute y(1) Error= help (numbers) help (numbers) Error Previous error help (numbers) The error went down by the factor: help (numbers) Euler's method is a first order method so we expect the error to go down by a factor of 0.5 each halving. Of course, that's only very approximate, so the numbers you get above are not exactly 0.5.