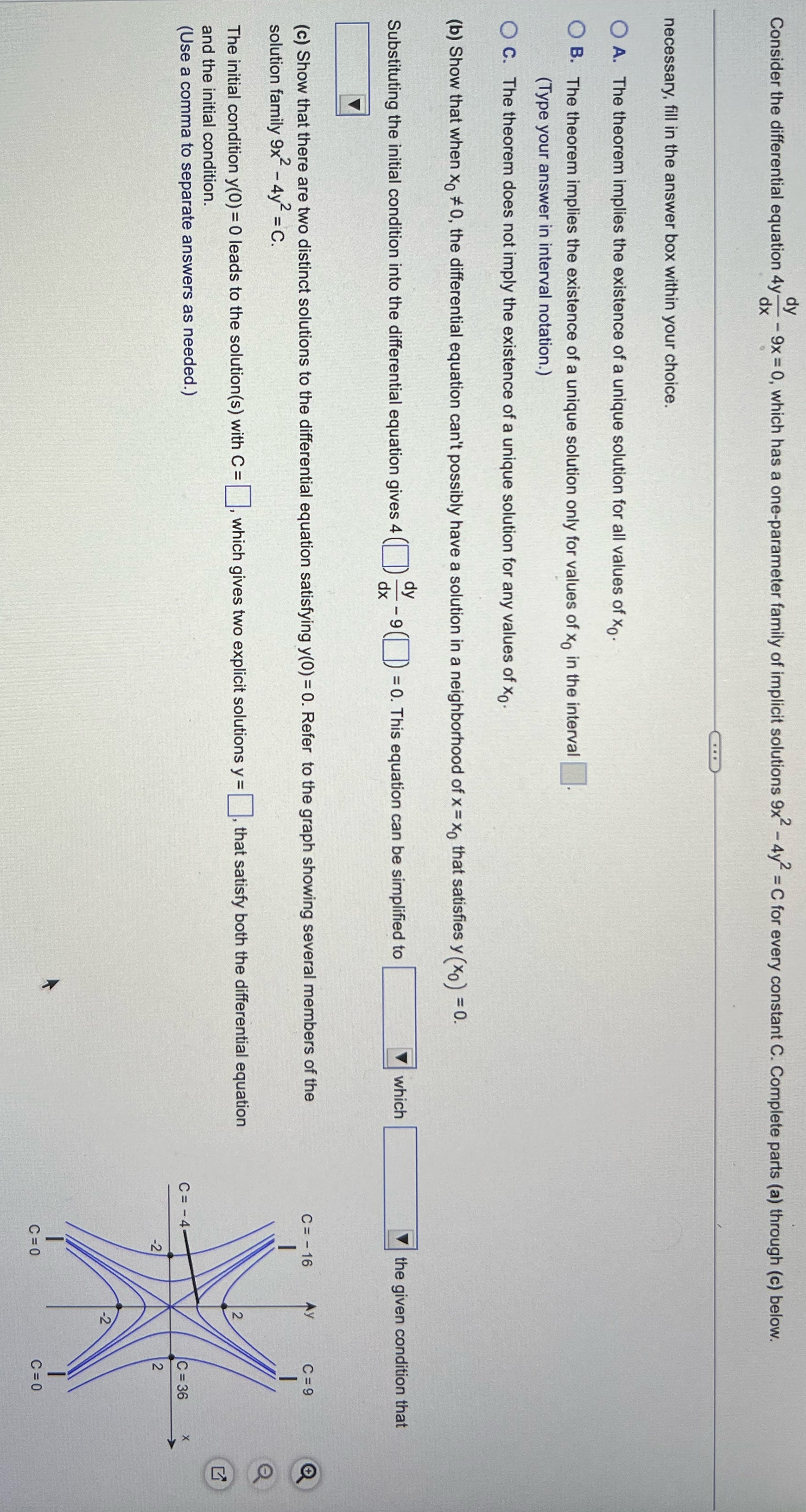
Consider the differential equation 4y dy - 9x =0, which has a one-parameter family of implicit solutions 9x2 - 4y- = C for every constant C. Complete parts (a) through (c) below. necessary, fill in the answer box within your choice. O A. The theorem implies the existence of a unique solution for all values of X . O B. The theorem implies the existence of a unique solution only for values of Xo in the interval (Type your answer in interval notation.) C. The theorem does not imply the existence of a unique solution for any values of x. (b) Show that when X #0, the differential equation can't possibly have a solution in a neighborhood of x = Xo that satisfies y (Xo ) = 0. Substituting the initial condition into the differential equation gives 4 (]) - 9 () = 0. This equation can be simplified to which the given condition that (c) Show that there are two distinct solutions to the differential equation satisfying y(0) = 0. Refer to the graph showing several members of the C = - 16 C=9 solution family 9x2 - 4y = C. The initial condition y(0) = 0 leads to the solution(s) with C = , which gives two explicit solutions y = , that satisfy both the differential equation and the initial condition. (Use a comma to separate answers as needed.) C= -4- C =36 4 C=0 C=0