Consider the differential equation dy/dx + xy = y^2, whose direction field is shown below.

Please show me step by step on following question in image.

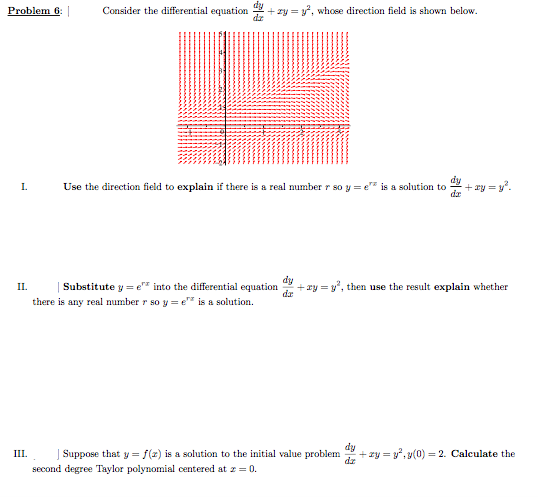
Problem G Consider the differential equation + + zy = y', whose direction field is shown below. Use the direction field to explain if there is a real number rao y = e" is a solution to = try =y'. IL. Substitute y = e" into the differential equation " + ry = y', then use the result explain whether there is any real number ~ so y = e" is a solution. III. Suppose that y = /(2) is a solution to the initial value problem " + zy =y',>(0) =2. Calculate the second degree Taylor polynomial centered at 2 = 0