Consider the (directed) network.

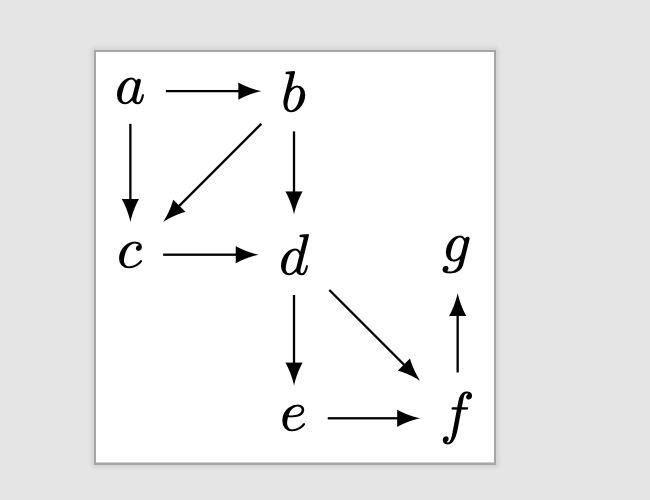
We could represent this network with the following Prolog statements:

link(a,b).

link(a,c).

link(b,c).

link(b,d).

link(c,d).

link(d,e).

link(d,f).

link(e,f).

link(f,g).

Now, given this network, we say that there is a `connection` from a

node `X` to a node `Y` if we can get from `X` to `Y` via a series of

links, for example, in this network, there is a connection from `a` to

`d`, and a connection from `c` to `f`, etc.

(a) Formulate the appropriate Prolog rule `connection(X,Y)` which is

true if (and only if) there is a `connection` from `X` to `Y` as

described above --- note that this rule will be recursive. Test this

rule out on the above network, to see if it is working correctly.

Once it is working correctly, you will note that, e.g., the query

`connection(a,e).` will give `true` multiple times. This means

something, actually:

a b d g e - f