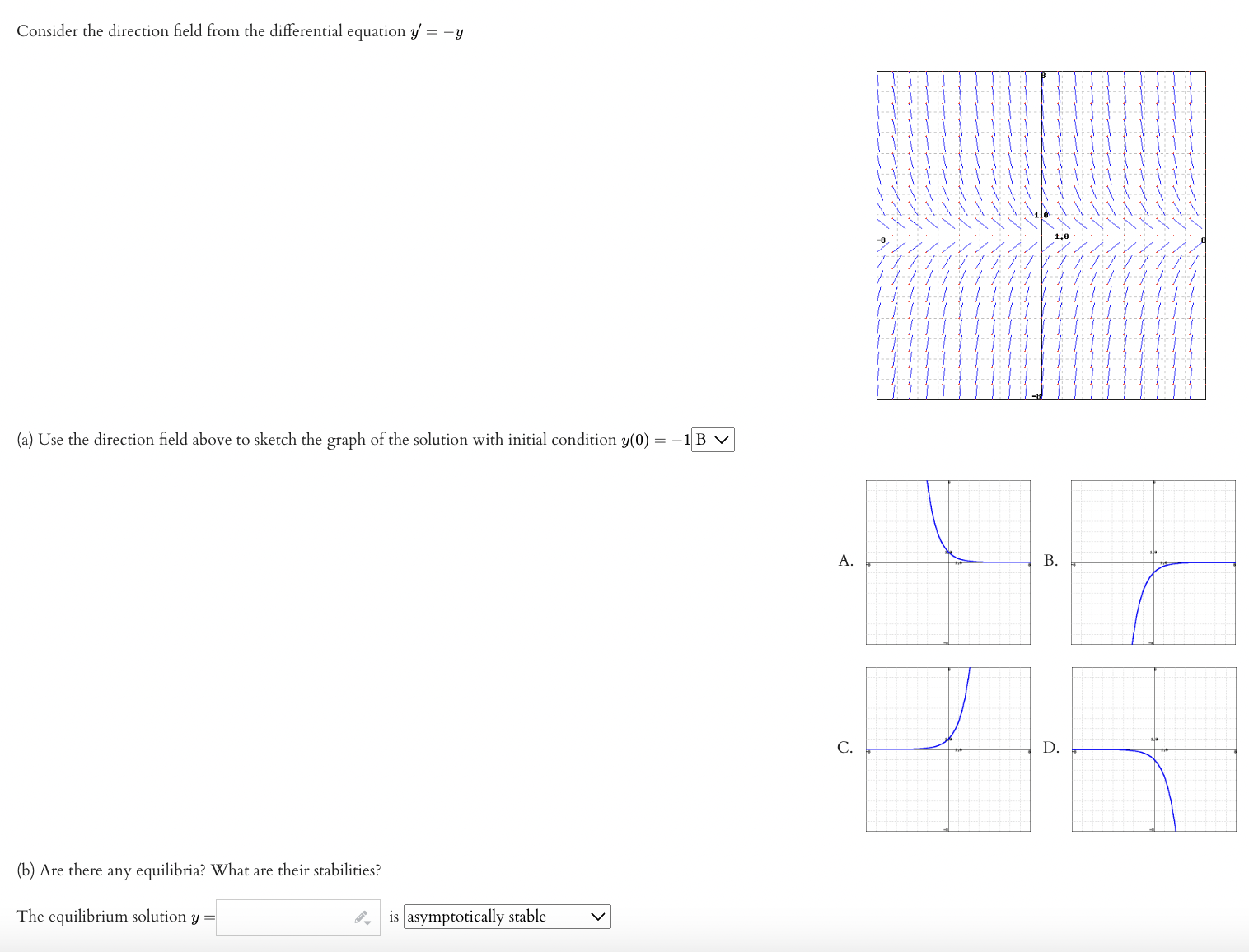
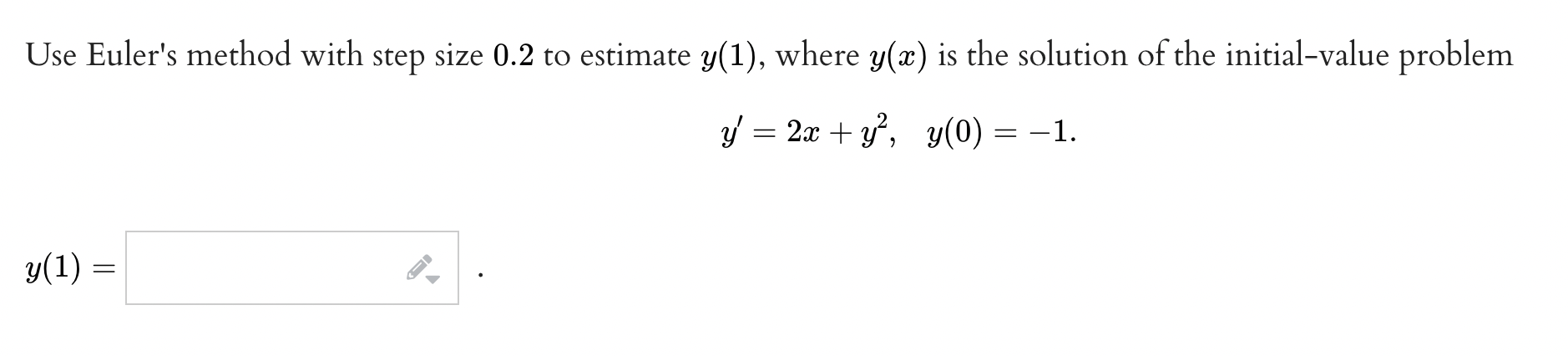
Consider the direction field from the differential equation y' = -y (a) Use the direction field above to sketch the graph of the solution with initial condition y(0) = -1 B V A. B. C. D. (b) Are there any equilibria? What are their stabilities? The equilibrium solution y = is asymptotically stable VUse Euler's method with step size 0.2 to estimate y(1), where y(w) is the solution of the initialvalue problem if = 23: +y2, y(0) = 1. Use Euler's method with the given step size to estimate y(1.4) Where y(a:) is the solution of the initialvalue problem y'= 5614;, 31(1) = 2- 1. Estimate y(1.4) With a step size h = 0.2. Answer: y(1.4) z y; 2. Estimate y(1.4) With a step size h = 0.1. Answer: y(1.4) z y; Consider the dinerential equation with initial condition y(0) = 2. A. Use Euler's method with two steps to estimate y when a: = 1: (Be sure not to round your calculations at each rtep!) Now use four steps: 21(1) z e: {Be sure not to round your calculations at each step!) B. What is the solution to this differential equation (with the given initial condition)? ' y: I. C. What is the magnitude of the error in the two Euler approximations you found? Magnitude of error in Euler with 2 steps = f, Magnitude of error in Euler with 4 steps = f, D. By what factor should the error in these approximations change (that is, the error with two steps should be what number times the error with four)? factor = i. {How close to this is the result you obtained above?)