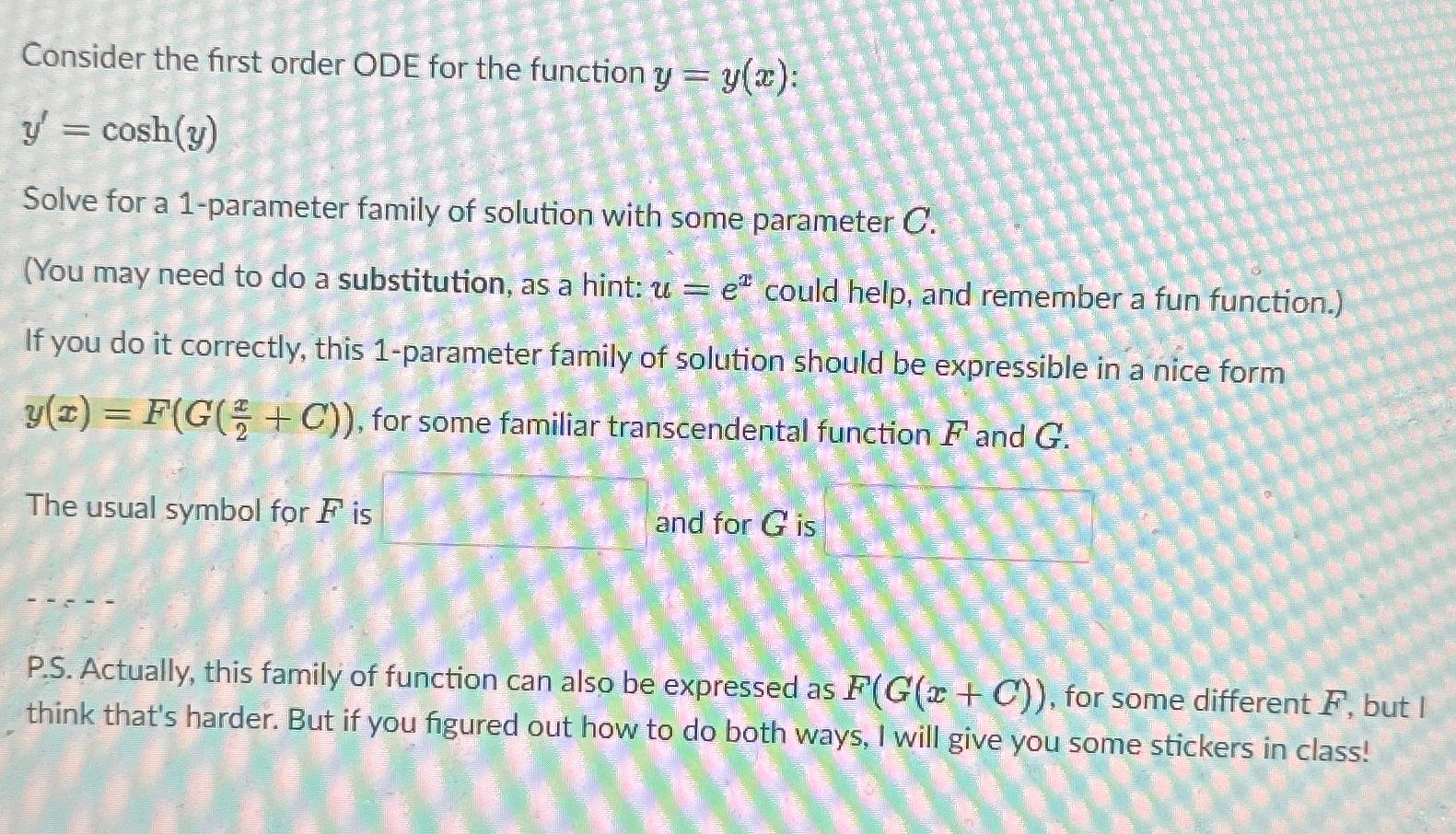
Question: Consider the first order ODE for the function y=y(x) : y^(')=cosh(y) Solve for a 1-parameter family of solution with some parameter C . (You
Consider the first order ODE for the function
y=y(x):\
y^(')=cosh(y)\ Solve for a 1-parameter family of solution with some parameter
C.\ (You may need to do a substitution, as a hint:
u=e^(x)could help, and remember a fun function.)\ If you do it correctly, this 1-parameter family of solution should be expressible in a nice form
y(x)=F(G((x)/(2)+C)), for some familiar transcendental function
Fand
G.\ The usual symbol for
Fis and for
Gis\ P.S. Actually, this family of function can also be expressed as
F(G(x+C)), for some different
F, but I think that's harder. But if you figured out how to do both ways, I will give you some stickers in class!
Consider the first order ODE for the function y=y(x) : y=cosh(y) Solve for a 1-parameter family of solution with some parameter C. (You may need to do a substitution, as a hint: u=ex could help, and remember a fun function.) If you do it correctly, this 1-parameter family of solution should be expressible in a nice form y(x)=F(G(2x+C)), for some familiar transcendental function F and G. The usual symbol for F is and for G is P.S. Actually, this family of function can also be expressed as F(G(x+C)), for some different F, but I think that's harder. But if you figured out how to do both ways, I will give you some stickers in class
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


