Question: Consider the following biobjective integer knapsack problem (BOIKP) maximize f(x) = [ f1(x) = 8x1 + 9x2 + 3x3, f2(x) = 3x1 + 2x2 +
Consider the following biobjective integer knapsack problem (BOIKP)
maximize f(x) = [ f1(x) = 8x1 + 9x2 + 3x3, f2(x) = 3x1 + 2x2 + 10x3 ]
s.t. 2x1 + 2x2 + 3x3
x1, x2, x3 > 0, integer
Note: All Pareto outcomes for this problem have integer components.
a) Use the weighted-sum method and/or the epsilon-constraint method and design an optimization process to compute all Pareto outcomes to this problem. Present the optimization process in the form of a multi-step procedure (pseudocode or flowchart) and explain why this process guarantees finding all Pareto outcomes.
b)Plot the computed Pareto outcomes in the objective space and include their coordinates.
c) Identify the supported and unsupported Pareto outcomes. Among the supported Pareto outcomes, identify extreme and nonextreme. Report the obtained efficient solutions and Pareto outcomes in the following table: 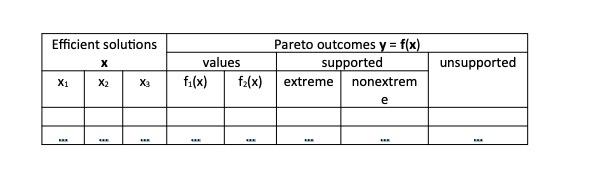
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


