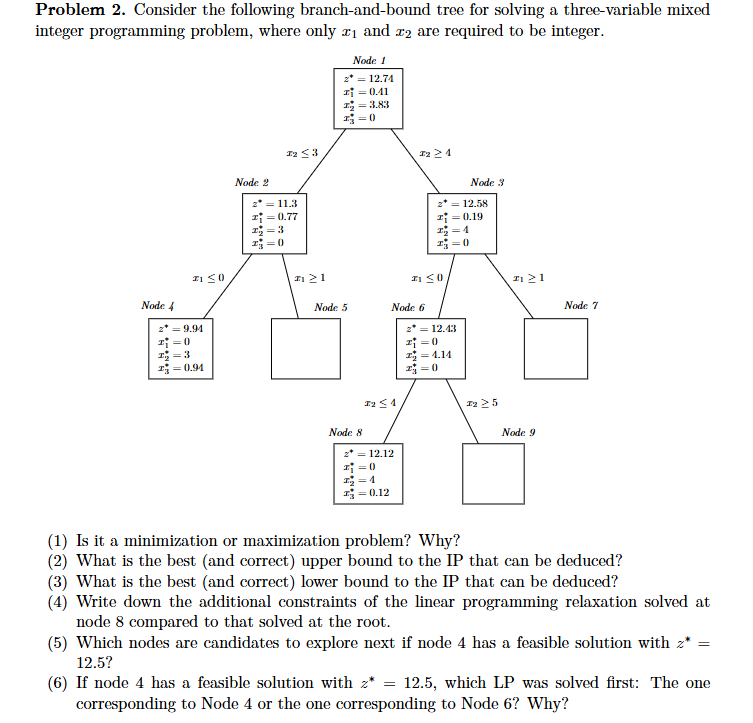
Consider the following branch$-$and$-$bound tree for solving a three$-$variable mixed

integer programming problem, where only x$1$ and x$2$ are required to be integer.Question $1(50)$ Consider the following MIP:

max z $=3$x $1+3$x $2+$x $3$

s$.$t$.3\mathrm{.}1$x $1+4\mathrm{.}1$x $2+5$x $317$

$6\mathrm{.}4$x $1+2\mathrm{.}7$x $2+3$x $313$

x $1,$ x $2,$ x $30$

x $1,$ x $2$ are integer

Below is a partial branch$-$and$-$bound tree used to solve the problem $($the nodes without any informa$-$

tion printed are nodes that have not been explored yet$).$

z $=12\mathrm{.}74$

x $$

$1=0\mathrm{.}41$

x $$

$2=3\mathrm{.}83$

x $$

$3=0$

Node $1$

z $=11\mathrm{.}3$

x $$

$1=0\mathrm{.}77$

x $$

$2=3$

x $$

$3=0$

Node $2$

z $=12\mathrm{.}58$

x $$

$1=0\mathrm{.}19$

x $$

$2=4$

x $$

$3=0$

Node $3$

z $=9\mathrm{.}94$

x $$

$1=0$

x $$

$2=3$

x $$

$3=0\mathrm{.}94$

Node $4$

z $=10\mathrm{.}33$

x $$

$1=1$

x $$

$2=2\mathrm{.}44$

x $$

$3=0$

Node $5$

z $=12\mathrm{.}43$

x $$

$1=0$

x $$

$2=4\mathrm{.}14$

x $$

$3=0$

Node $6$

z $=$ Inf

x $$

$1=$ Inf

x $$

$2=$ Inf

x $$

$3=$ Inf

Node $7$

z $=12\mathrm{.}12$

x $$

$1=0$

x $$

$2=4$

x $$

$3=0\mathrm{.}12$

Node $8$

z $=$ inf

x $$

$1=$ inf

x $$

$2=$ inf

x $$

$3=$ inf

Node $9$

x $23$ x $24$

x $10$ x $11$ x $10$ x $11$

x $24$ x $25$

$1.(+10)$ What is the best feasible solution to the MIP found so far?

$2$

$(1)$ Is it a minimization or maximization problem? Why?

$(2)$ What is the best $($and correct$)$ upper bound to the IP that can be deduced?

$(3)$ What is the best $($and correct$)$ lower bound to the IP that can be deduced?

$(4)$ Write down the additional constraints of the linear programming relaxation solved at

node $8$ compared to that solved at the root.

$(5)$ Which nodes are candidates to explore next if node $4$ has a feasible solution with z$=$

$12\mathrm{.}5?$

$(6)$ If node $4$ has a feasible solution with z$=12\mathrm{.}5,$ which LP was solved first: The one

corresponding to Node $4$ or the one corresponding to Node $6?$ Why? Problem $2.$ Consider the following branch$-$and$-$bound tree for solving a three$-$variable mixed integer programming problem, where only $\backslash ($ x$\_\{1\}\backslash )$ and $\backslash ($ x$\_\{2\}\backslash )$ are required to be integer.

$(1)$ Is it a minimization or maximization problem? Why?

$(2)$ What is the best $($and correct$)$ upper bound to the IP that can be deduced?

$(3)$ What is the best $($and correct$)$ lower bound to the IP that can be deduced?

$(4)$ Write down the additional constraints of the linear programming relaxation solved at node $8$ compared to that solved at the root.

$(5)$ Which nodes are candidates to explore next if node $4$ has a feasible solution with $\backslash ($ z$^\{*\}=\backslash )12\mathrm{.}5?$

$(6)$ If node $4$ has a feasible solution with $\backslash ($ z$^\{*\}=12\mathrm{.}5\backslash ),$ which LP was solved first: The one corresponding to Node $4$ or the one corresponding to Node $6?$ Why?