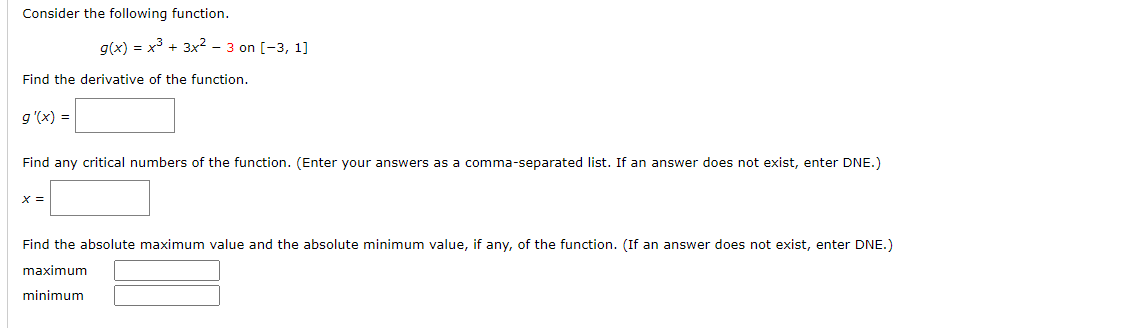
Question: Consider the Following function. 900 = x3 + 3x2 3 on [3, 1] Find the derivative of the function. 9'{X} = Find any critical numbers
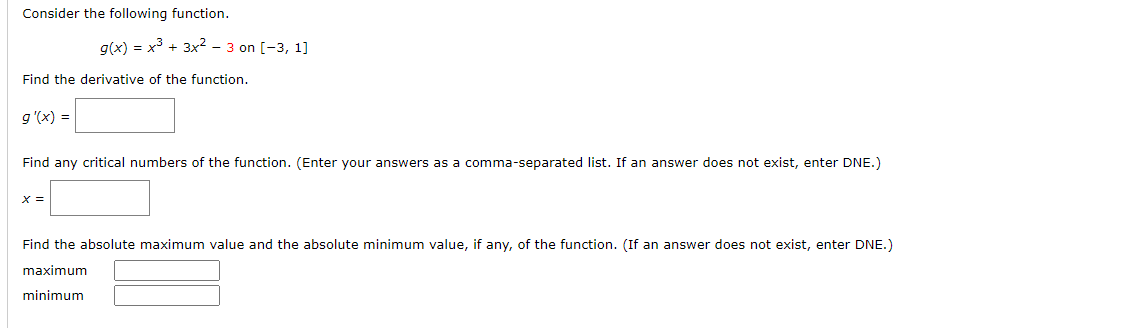
![[3, 1] Find the derivative of the function. 9'{X} = Find any](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667d1495f025a_301667d1495daf92.jpg)
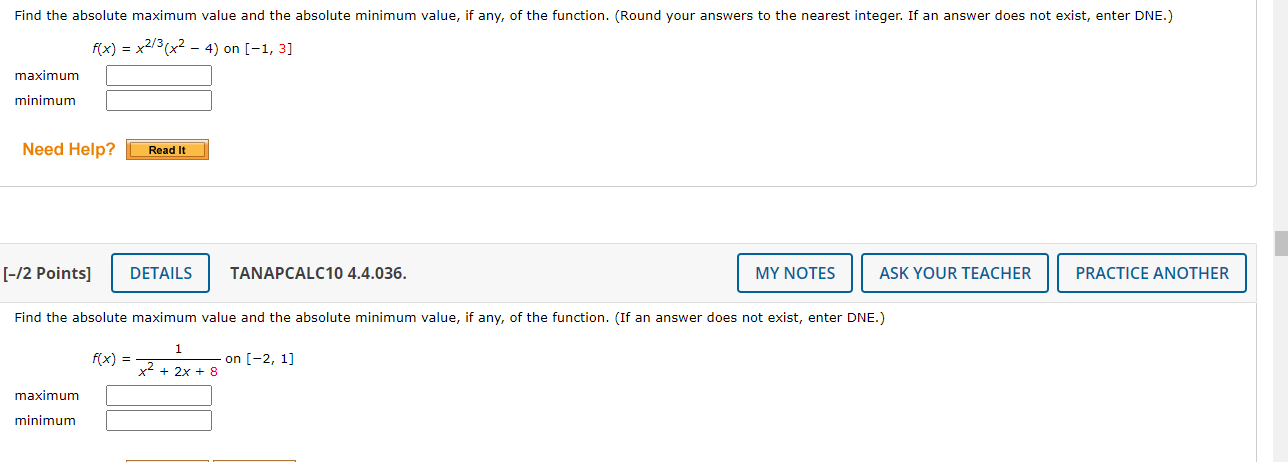


![the following function. 90} = 0n [7. 9] fS Find the derivative](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667d14977e40f_303667d14976ab49.jpg)
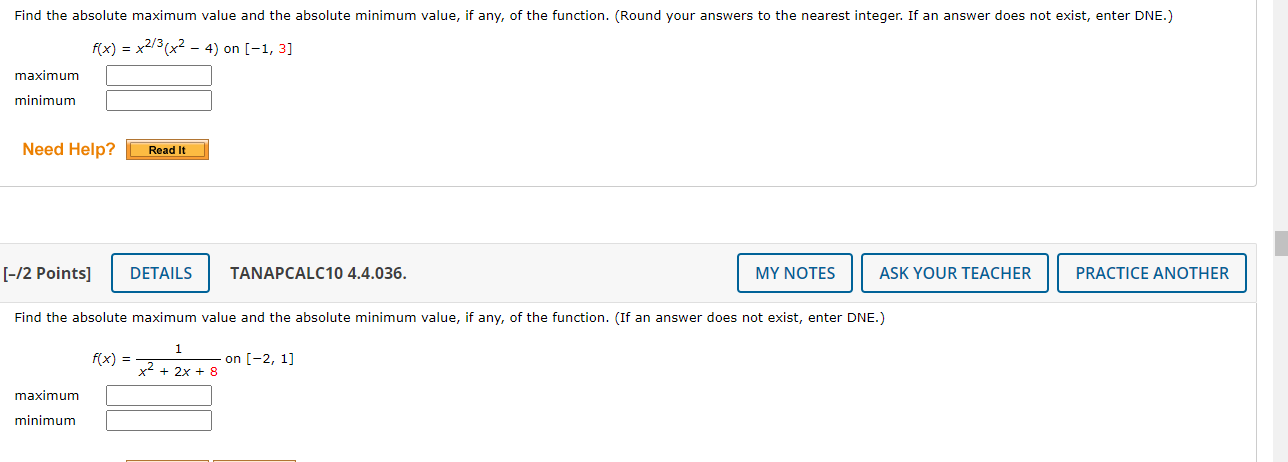


Consider the Following function. 900 = x3 + 3x2 3 on [3, 1] Find the derivative of the function. 9'{X} = Find any critical numbers of the function. {Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) Find the absolute maximum value and the absolute minimum value, if any, of the function. (If an answer does not exist, enter DNE.) maximum E mmmum E Consider the following function. 90} = 0n [7. 9] fS Find the derivative of the function. Q'U') = Find any critical numbers of the function. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) t: Find the absolute maximum value and the absolute minimum value, if any, of the function. (If an answer does not exist, enter DNE.) maximum E mmmum E Find the absolute maximum value and the absolute minimum value, if any, of the function. (Round your answers to the nearest integer. If an answer does not exist, enter DNE.) x) = x130? 4) on [1, 3] maximum |:| mmmum |:| Need Help? [42 Points] DETAILS TANAPCALC1O 4.4.035. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Find the absolute maximum value and the absolute minimum value, if any, of the function. (If an answer does not exist, enter DNE.) 1 x)=2on [-2. 1] x +2x+8 maximum E mmmum E The altitude (in feet) attained by a model rocket t seconds into flight is given by the function h(t). Find the maximum altitude attained by the rocket. h(t) = - _+ + 5+2 + 24t + 20 (t 20) Click here to begin!The quantity:I demanded each month of the Walter Serkin recording of Beethoven's Moonlight Sonata, produced by Phonola Media, is related to the price per compact disc. The equation p = o.00054x+ 6 (o s xs 12,000) where ,0 denotes the unit price in dollars and xis the number of discs demanded, relates the demand to the price. The total monthly cost {in dollars] for pressing and packaging X copies ofthis classical recording is given by C(x) = 500 + 2x , 0.00001):2 (o 5 x 3 20,000}. Hint: The revenue is R[x) : px, and the prot is P[x) : R(x) C(x). Find the revenue function, R(x) : px. R(x) = Find the prot Function, P(x) = R(x) C(x). Pix} = Find the derivative of the prot function, P[x). P'(x) = Find the critical number of the function P(x}. (Round your answer to the nearest whole number.) To maximize its prots, how many copies should Phonola produce each month? (Round your answer to the nearest whole number.)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


