Question: Consider the following function and closed interval. f(x) = x- 4x - 16x + 5, [-4, 4] Is f continuous on the closed interval

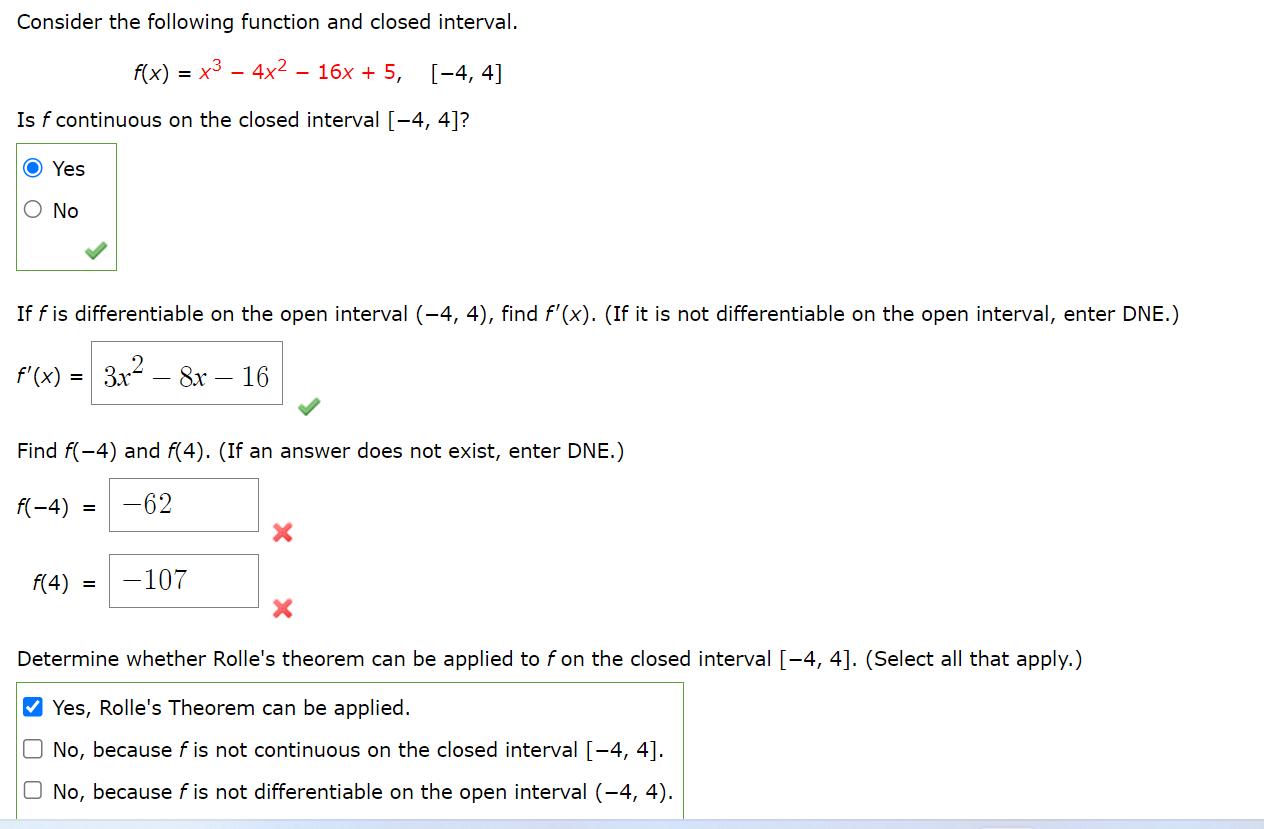
Consider the following function and closed interval. f(x) = x- 4x - 16x + 5, [-4, 4] Is f continuous on the closed interval [-4, 4]? Yes No If f is differentiable on the open interval (-4, 4), find f'(x). (If it is not differentiable on the open interval, enter DNE.) f'(x) = 3x- 8x-16 Find f(-4) and f(4). (If an answer does not exist, enter DNE.) f(-4) f(4) = = -62 -107 Determine whether Rolle's theorem can be applied to f on the closed interval [-4, 4]. (Select all that apply.) Yes, Rolle's Theorem can be applied. No, because f is not continuous on the closed interval [-4, 4]. No, because f is not differentiable on the open interval (-4, 4).

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

When select mining method, the technical factors include 1 . recovery 2 . dilution 3 . flexibility 4 . selectivity 5 . conentration or dipersion of working 6 . capital and labor intensities. Please...

For the year just completed, Hanna Company had net income of $99,000. Balances in the companys current asset and current liability accounts at the beginning and end of the year were as follows:...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

In an organization that has high employee satisfaction, ______. Multiple choice question. customer interactions are forced and scarce employee turnover is high more positive interactions take place...

(a) What two cryptographic protections does an HMAC provide? (b) Do HMACs use symmetric key encryption, public key encryption, or hashing? (c) What is the benefit of HMACs over digital signatures?

What are the three questions marketing executives consider when choosing a marketing channel and intermediaries? AppendixLO1

Does the person have her/his vita posted?

The city of Segovia is contemplating building a second airport to relieve congestion at the main airport and is considering two potential sites X and Y. Hard Rock Hotels would like to purchase land...

Salmone Company reported the following purchases and sales of its only product Salmone uses a periodic inventory system. Determine the cast assigned to cost of goods sold using FIFO. Units Sold at...

A severe winter ice storm has swept across North Carolina and Virginia, followed by over a foot of snow and frigid, single-digit temperatures. These weather conditions have resulted in numerous...

96) 1 day before closing the seller says the contract was breached & he won't close. the buyer says documents are signed money paid & the signed deed is in escrow. There is no breach. Escrow should:...

1. Your father knows that last week you have learned jointly distributed random variables from Aybek Hoca. He has asked you to calculate certain distributions and expectations. Please let X denote...

There Were Ethical Dilemmas All Day Long," in your opinion, should a researcher conduct an ethnographic research study even if he or she acknowledges that he cannot be objective or unbiased during...

From this article Could you help me to identify and pick it from one of the two ERM quadrants that are typically speculative in nature - and explain what the risk is, why it is speculative, and why...

The company Techito S.A. has the following cost elements: 1. Rental of premises or office 2. Social charges on wages paid for production. 3. Purchase of glue and staples for reinforced section 4....

Design a Hazard Communication Programme use the link https://www.osha.gov/sites/default/files/2018-12/fy10_sh-21003-10_mod_2_hazcom_program.pdf LITERATURE Review of literature on significant...

4 3 . _ _ _ _ _ _ _ _ _ _ pipe is the most suitable for carrying sanitary drainage. Stainless steel Reinforced cement concrete Cast iron Asbestos cement

Gordon and Lisa estimate that they will need $1,875,000 in 40 years for their retirement years. If they can earn 8 percent annually on their funds, how much do they need to save annually?

For each transition matrix P in Problem, solve the equation SP = S to find the stationary matrix S and the limiting matrix 12

Show that y = x2 + C is a solution of the differential equation dy/dx = x/y for any real number C. Find the particular solution that passes through (-6,7).

Three departments have 12, 15, and 18 members, respectively. If each department selects a delegate and an alternate to represent the department at a conference, how many ways can this be done?

Regular investments made at the beginning of each quarter earn 6% compounded quarterly. How many more $1000 investments than $1100 investments will it take to accumulate $100,000?

Suppose that $5000 is contributed at the beginning of each year for 25 years to an RRSP that earns 10% compounded annually. By what percentage would annual contributions have to be increased in order...

An RRSP is now worth $316,000 after contributions of $3500 at the beginning of every six months for 17 years. What effective rate of return has the plan earned?