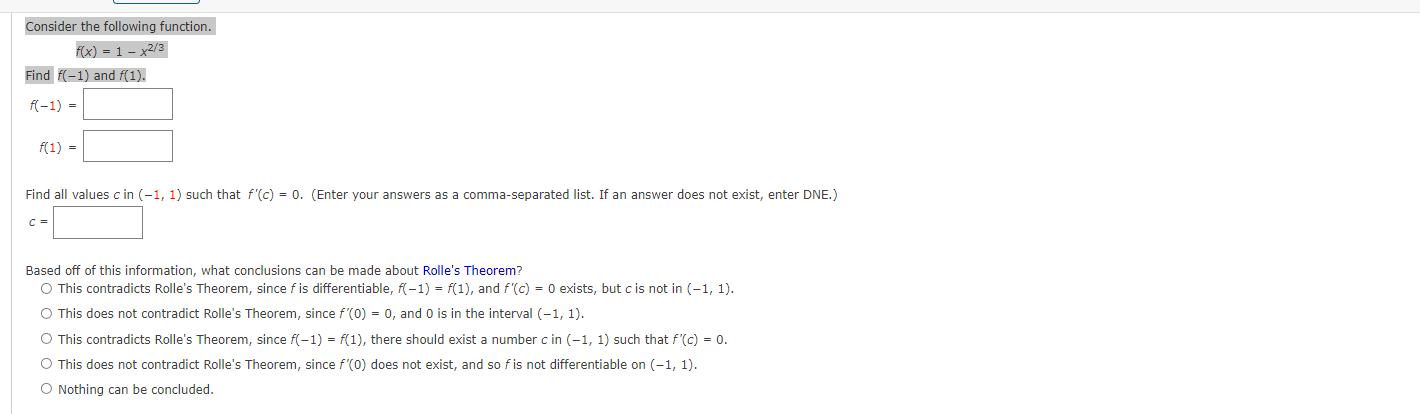
Consider the following function. f(x) = 1-x2/3 Find f(-1) and f(1). f(-1) = f(1) Find all values c in (-1, 1) such that f'(c) = 0. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) C = Based off of this information, what conclusions can be made about Rolle's Theorem? This contradicts Rolle's Theorem, since f is differentiable, f(-1) = f(1), and f'(c) = 0 exists, but c is not in (-1, 1). This does not contradict Rolle's Theorem, since f'(0) = 0, and 0 is in the interval (1, 1). This contradicts Rolle's Theorem, since f(-1) = f(1), there should exist a number c in (-1, 1) such that f'(c) = 0. This does not contradict Rolle's Theorem, since f'(0) does not exist, and so f is not differentiable on (-1, 1). O Nothing can be concluded.