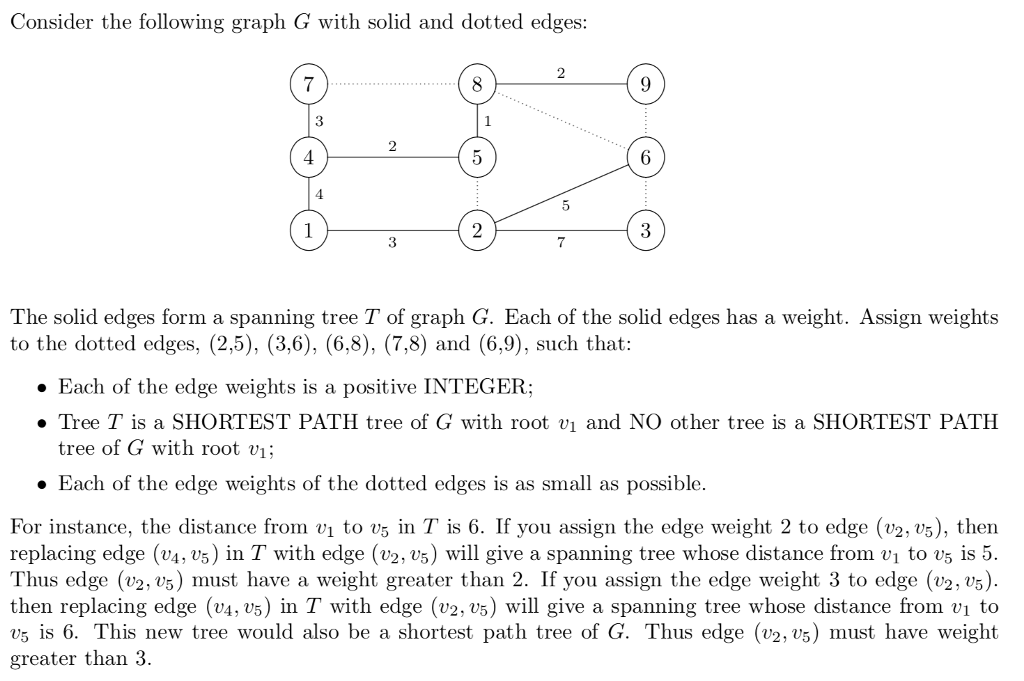
Consider the following graph G with solid and dotted edges: 3 6 The solid edges form a spanning tree T of graph G. Each of the solid edges has a weight. Assign weights to the dotted edges, (2,5), (3,6), (6,8), (7,8) and (6,9), such that: Each of the edge weights is a positive INTEGER; Tree T is a SHORTEST PATH tree of G with root vi and NO other tree is a SHORTEST PATH tree of G with root vi; Each of the edge weights of the dotted edges is as small as possible. For instance, the distance from vi to v5 in T is 6. If you assign the edge weight 2 to edge (v2, v5), then replacing edge (v4, vs) in T with edge (v2, v5) will give a spanning tree whose distance from v1 to vs is 5. Thus edge (v2, v5) must have a weight greater than 2. If you assign the edge weight 3 to edge (v2, v5) then replacing edge (v4, v5) in T with edge (v2, v5) will give a spanning tree whose distance from vi to v5 is 6. This new tree would also be a shortest path tree of G. Thus edge (v2, v;) must have weight greater than 3