Question: Consider the following graph where the nodes J = {3,5,6,7,8} in dashed boxes are possible facility locations, the nodes I = {1,2,4,9,10} are customers,

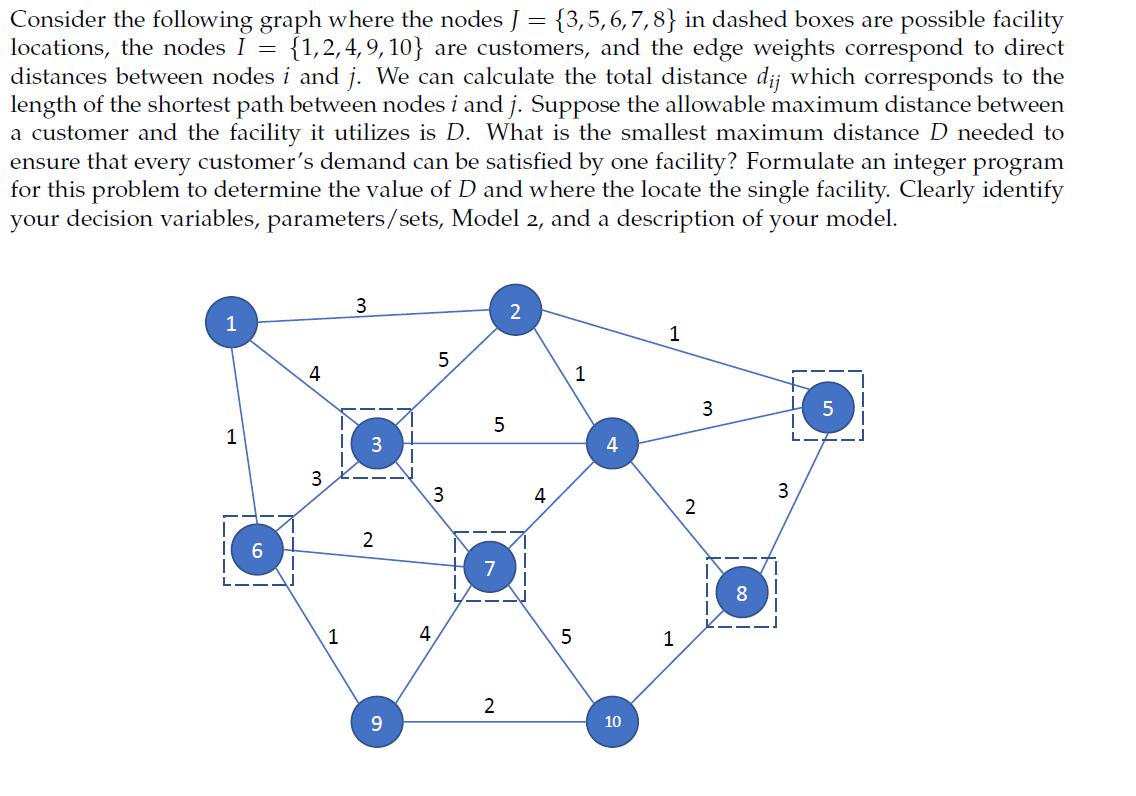
Consider the following graph where the nodes J = {3,5,6,7,8} in dashed boxes are possible facility locations,

Consider the following graph where the nodes J = {3,5,6,7,8} in dashed boxes are possible facility locations, the nodes I = {1,2,4,9,10} are customers, and the edge weights correspond to direct distances between nodes i and j. We can calculate the total distance dj which corresponds to the length of the shortest path between nodes i and j. Suppose the allowable maximum distance between a customer and the facility it utilizes is D. What is the smallest maximum distance D needed to ensure that every customer's demand can be satisfied by one facility? Formulate an integer program for this problem to determine the value of D and where the locate the single facility. Clearly identify your decision variables, parameters/sets, Model 2, and a description of your model. 1 1 4 3 1 3 3 2 9 4 5 3 5 2 4 1 5 10 1 1 2 3 8 3 5

Step by Step Solution

★★★★★

3.46 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

I have read and understood the question and answer on Cheggcom that you linked The question asks for ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

The flowchart in Figure depicts part of a clients revenue cycle. Some of the flowchart symbols are labeled to indicate control procedures and records. For each symbol numbered1 through 13, select one...

In terms of land area - total and average size - more can be found with what recreational areas than others?

What is the spring cloud API Gateway and how do you set it up to make a call to the product service via eureka service discovery server? Give me the complete code in detailed steps.

Design a controller to stabilize the system G(S) = with feedback H(S) +371

AND 1. THE USE OF CALCULATORS SPREAASHEETS 2. PLEASE MAKE SURE TO WRITE Stolal ANSWER EXPLANATIONS THAT ARE SUPPORTED BY YOUR CALCULATIONS deep AsE OuESTION 3. PLEASE USE EXCEL TO CALCULATE AND SHOW...

HELP ME WITH RISK ASSESSMENT,analysis company: GOOGLE INC. UNDERSTANDING THE ENTITY AND ITS ENVIRONMENT: COMPLEX ENTITIES PURPOSE This form has been designed to assist the auditor in: Gathering audit...

ATC 14-1 (Pg. 686) 1.(Follow the cash) In a narrative format, answer the questions posed in the case. 2.What is meant by "presentation of financial statement information in common-size amounts rather...

i need 5 balance sheets for Auto Zone company from the resources "attachments and the link below" for the last 5 years, 2011-2012-2013-2014-2015 with the sixth page including the total income and...

this is the question about financial economics, my group already finished all of questions and left (g) and (i) . I will upload my word and excel for question data and group work, please add your...

Critique the regulators use of cost in assessing whether predatory pricing of fuel has occurred. Explain whether you think the judge should lift the injunction on Fill n Shop, following consideration...

Sign Test for Freshman 15 The table below lists some of the weights from Data Set 4 in Appendix B. Those weights were measured from college students in September and later in April of their freshman...

How do you explain that Mb saturates faster than Hb, explain with the help of a graph.

IFRS 1 5 , Revenue from Contracts with Customers, covers which types of revenues? State of Boodis Rendering of services Rovalties All of the above Question 1 5 Which of the following is NOT a...

Which preventive, detective, and/or corrective controls would best mitigate the following threats? a. An employees laptop was stolen at the airport. The laptop contained personally identifying...

1. A company had stock outstanding as follows during each of its first three years of operations: 2,500 shares of $10, $100 par, cumulative preferred stock and 50,000 shares of $10 par common stock....

Determine consolidated taxable income for the calendar year Yeti Group, which elected consolidated status immediately upon the creation of the two member corporations on January 1 of year 1. All...

On January 1, 2017, Xiamen Company made amendments to its defined benefit pension plan that resulted in 60,000 yuan of past service cost. The plan has 5,000 active employees with an average expected...

On April 1, 10,000 shares of $5 par common stock were issued at $25, and on April 7, 5,000 shares of $50 par preferred stock were issued at $103. Journalize the entries for April 1 and 7.

If you need to replan during a nine-month project, what is typically the best time to ask the customer for more time or money?Select an answer:at the moment the plan goes off trackduring the last...

Use predictorcorrector to integrate subject to the initial condition y(0) = 1. dy dx =xy/2 (4.2.53)

Consider the nonlinear ordinary differential equation with y(0) = 1. Estimate y(1) (a) Using the explicit Eulers method with h = 0.2 (b) Using the fourth-order RungeKutta method with h = 1. dy dx ||...

Use Picards method to find the roots of for the initial guesses 0.1, 0.6, 1.99, and 2.01. f(x)=x-3x+2=0 (3.3.2)

The distribution of N in (13.1) is often not approximately normal. The distribution of = m/n2, however, is often close to normality, and CIs for p are easily constructed. For the data in Example...

a. For Chapmans estimator in (13.2), let X be the random variable denoting the number of marked individuals in the second sample. What is the probability distribution of X? b. Show that E[] = N if...

Bellemain et al. (2005) relied on moose hunters in Norway to collect fecal samples from brown bears. Each sample was genotyped, and the number of distinct individuals was found in each of 2001 and...