Question: Consider the following interpretation in predicate logic: Domain ={ fluffy, thumper, joe, rover, bill, duke, louie, shy, happy } Predicates: R= rabbit, and is true

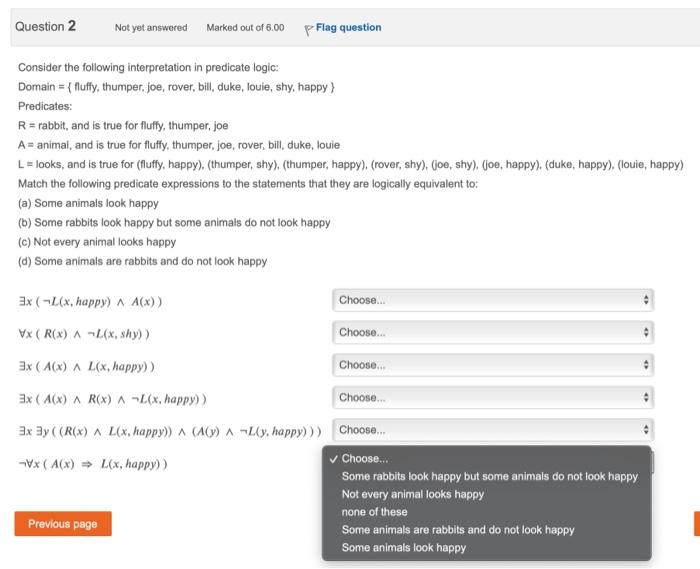
Consider the following interpretation in predicate logic: Domain ={ fluffy, thumper, joe, rover, bill, duke, louie, shy, happy } Predicates: R= rabbit, and is true for fluffy, thumper, joe A= animal, and is true for fluffy, thumper, joe, rover, bill, duke, louie L= looks, and is true for (fluffy, happy), (thumper, shy), (thumper, happy), (rover, shy), (joe, shy), (joe, happy), (duke, happy), (louie, happy) Match the following predicate expressions to the statements that they are logically equivalent to: (a) Some animals look happy (b) Some rabbits look happy but some animals do not look happy (c) Not every animal looks happy (d) Some animals are rabbits and do not look happy x(L(x,happy)A(x)) x(R(x)L(x,shy)) x(A(x)L(x,happy)) x(A(x)R(x)L(x, happy )) xy((R(x)L(x, happy ))(A(y)L(y, happy ))) x(A(x)L(x, happy ))

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Consider the following interpretation in predicate logic: Domain = { fluffy, thumper, joe, rover, bill, duke, louie, shy, happy } Predicates: R= rabbit, and is true for fluffy, thumper, joe A=...

Consider the following interpretation for propositional functions P, Q and R with domain D = {1,2,3,4,5,6}. In parts (i) (iv) you are given formulae in predicate logic. You are required to give the...

forgot to put the begining of the quistion Styles to give the truth values and explain why these formulae have such truth values. x P(x) Q(x) R(x) F T T N F F T 3 T F T 4 T F T 5 T F F 6 T T T Give...

1. Consider the following models of finite geometries. You may assume that cach dark circle is a point and cach line that looks like a line is a line in the model. Determine which of the following...

Consider the following interpretation of incidence geometry. Begin with a punctured sphere in Euclidean three-space, i.e., a sphere with one point N removed. Interpret "points" as points on the...

Consider the two-period model of consumption and saving that we described in class. Consider the following interpretation of the model. The first period corresponds to the working period of life, and...

Consider the following interpretation of a geometry. Begin with a punctured sphere in Euclidean 3-space. This is a sphere with one point, P , removed, where everything else about the sphere looks...

3-2 Rite Aid Inventory Surplus Fraud Occupational Fraud comes in many shapes and sizes. The fraud at Rite Aid is one such case. On February 10 th , 2015, the US Attorney?s Office for the Middle...

ars ess The Brod Tools the properto entreprise en troductory The better with pore The masse smyyn, omstret In maleng capital structure decision, matargers must manage the following leverage for...

8:27 Tue, Jul 23 2 0. OK S. 649% Expanding the Net Present Value Method LO2 . Know CCB: Prepare an NPV analysis of two competing projects using either the total cost approach or the incremental cost...

Many manufacturing problems involve the matching of machine parts, such as shafts that fit into a valve hole. A particular design requires a shaft with a diameter of 22.000 mm, but shafts with...

Which statement is incorrect? Explain. a. Correlation uses a t-test with n 2 degrees of freedom. b. Correlation analysis assumes that X is independent and Y is dependent. c. Correlation analysis is...

30. Statement I. Inventory computerization has tended to reduce inventory levels. Statement II. Inventory investment tends to rise during recessions. (LO5) a) Statement I is true and statement II is...

5. Develop a scenario comparing two PH programs and involving the use of a CBA.

(Appendices) PREPARATION OF MERCHANDISING FINANCIAL STATEMENTS. Jay Coat Company has prepared the following unadjusted trial balance as of December Ble Ox2: LO9 The following data are also available:...

(Appendices) UNCOLLECTIBLE ACCOUNT EXPENSE: CREDIT SALES METHOD. The Glass House, a glass and china store, sells nearly half its merchandise on credit. During the past 4 years, the following data...

(Appendices) PURCHASES AND PURCHASES RETURNS. On November 6, Lubin Products purchased on credit 350 parts kits from Michaels Electronics for $38 per kit. Michaels paid $320 to have the kits shipped...