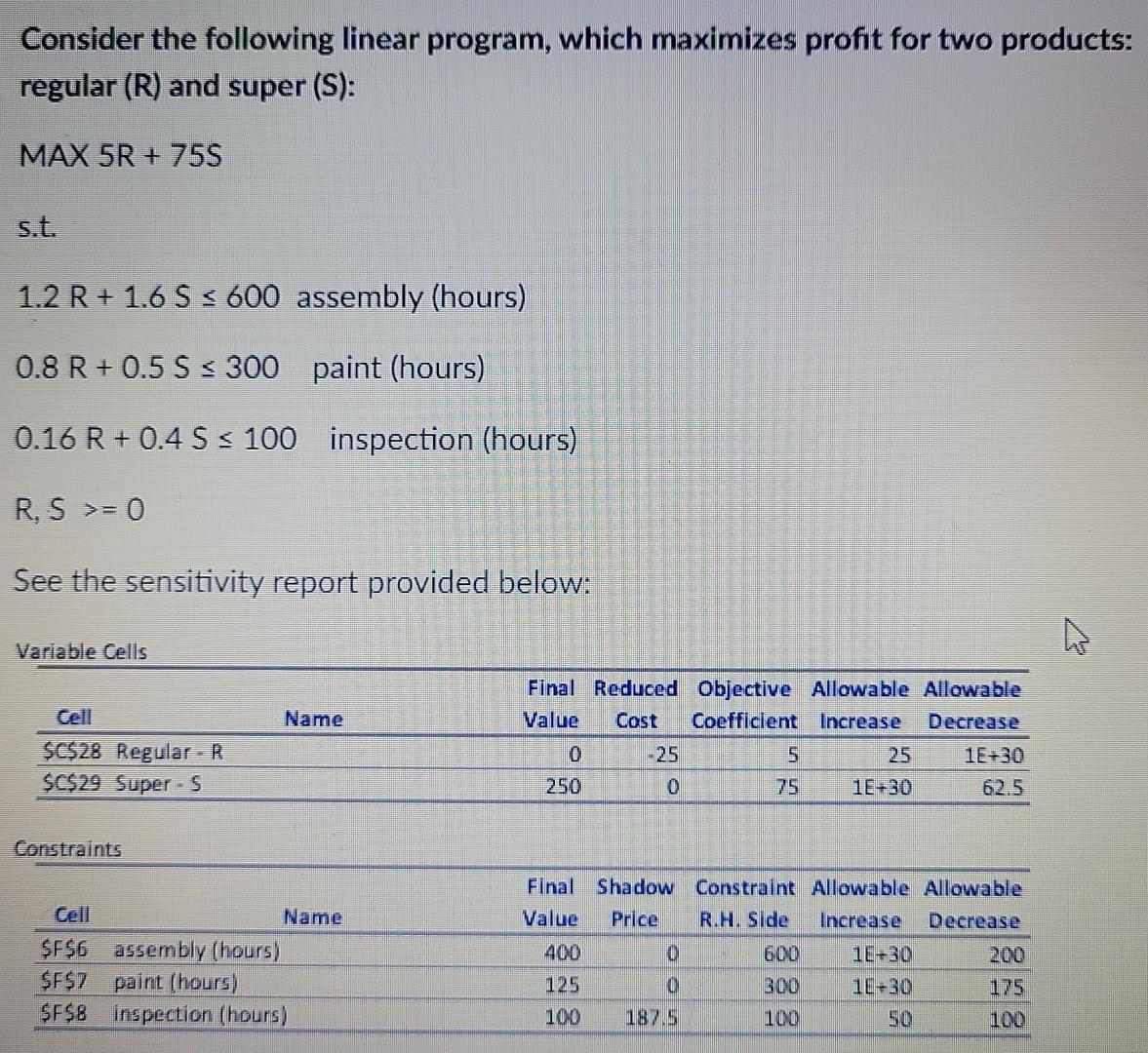
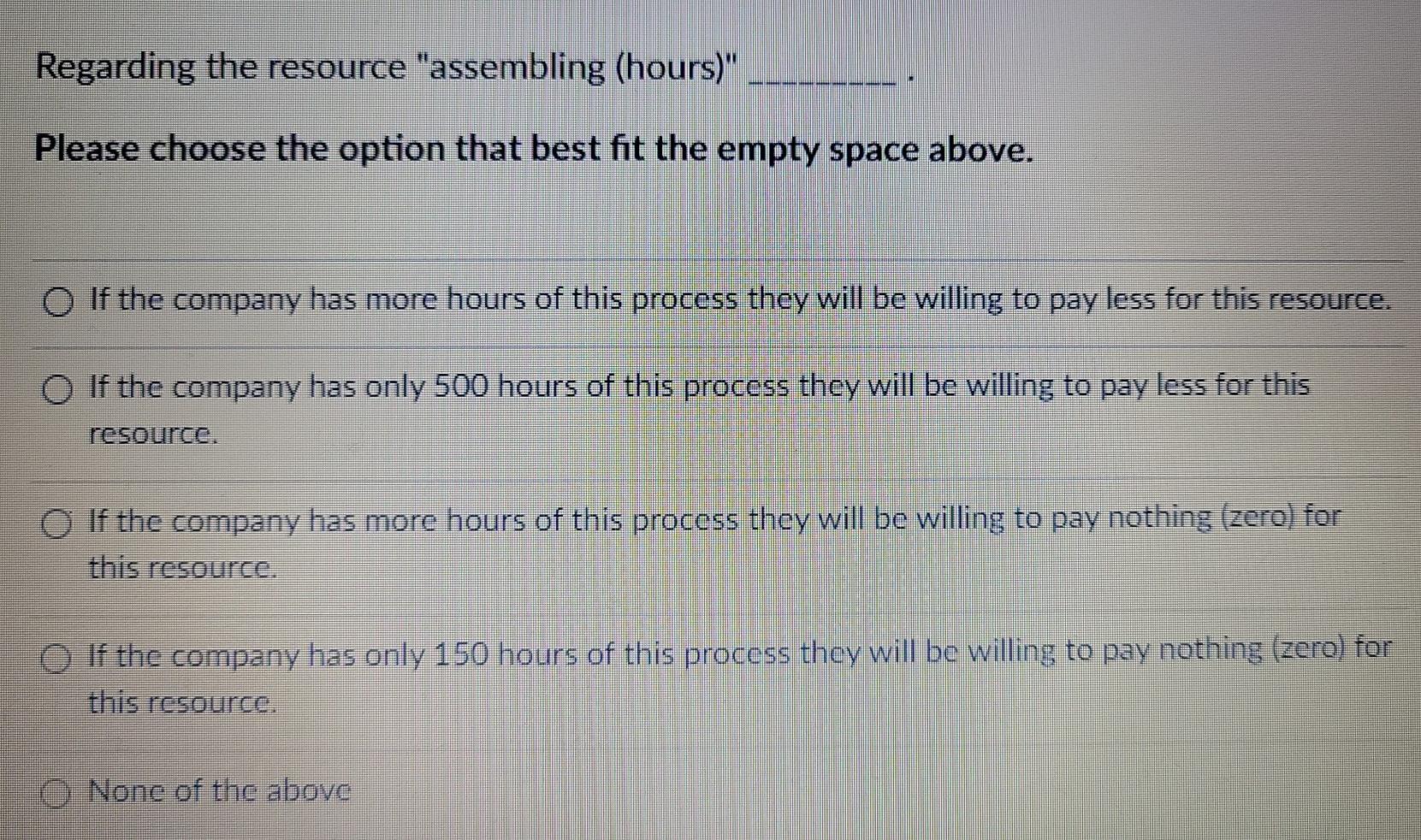
Consider the following linear program, which maximizes profit for two products: regular (R) and super (S): MAX 5R + 755 s.t. 1.2 R+ 1.6 S s 600 assembly (hours) 0.8 R +0.5 S = 0 See the sensitivity report provided below: Variable Cells Name $C$28 Regular - R $C$29 Super -S Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 0 25 250 0 1E+30 Constraints Name $F$6 assembly (hours) $F$7 paint (hours) $F$8 inspection (hours) Final Shadow Constraint Allowable Allowable Value Price R.H side Increase Decrease 400 0 600 11+30 200 OI 300 10+30 100 187.5 100 50 100 Regarding the resource "assembling (hours)" Please choose the option that best fit the empty space above. O If the company has more hours of this process they will be willing to pay less for this resource. O If the company has only 500 hours of this process they will be willing to pay less for this resource. If the company has more hours of this process they will be willing to pay nothing (zero) for this resource. O If the company has only 150 hours of this process they will be willing to pay nothing (zero) for this resource. None of the above