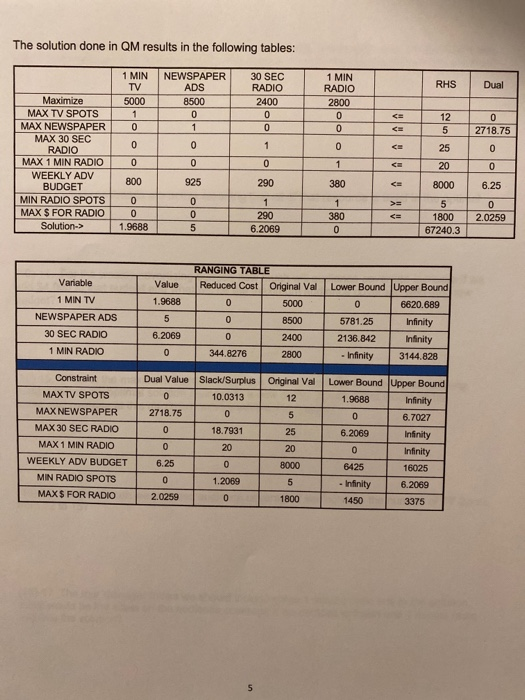
Consider the following linear programming problem for questions 12.17 The Arizona Travel Club sponsors trips to the Hawaiian Islands. They want to determine how to reach the maximum number of potential customers. Below are the available data. - $8,000 per week to spend on advertising - Goal is to reach the largest possible high-potential audience - Media types and audience figures shown below - Place at least five radio spots per week - No more than $1,800 can be spent on radio advertising each week The LP formulation is below. The QM solution with Ranging Table is shown on Page 4. There are 6 questions on Page 5 using the QM tables. Use the decimal form of the results - don't try to convert to integers. Note that there is one >= constraint (Minimum number of radio spots. X1 = number of 1-minute TV spots taken each week X2 = number of daily newspaper ads taken each week X3 = number of 30-second prime-time radio spots taken each week X4 number of 1-minute afternoon radio spots taken each week Objective Function: Maximize audience coverage = 5,000X1 + 8,500X2 + 2,400X3 + 2,800X4 Subject to X1 S 12 (max TV spots/week) X2 55 (max newspaper ads/week) X: S25 (max 30-sec radio spots/week) X4 S20 (max 1-min radio spots/week) 800X: +925X2 + 290X: + 380X4 5 $8,000 (weekly advertising budget) X + X 25 (min radio spots contracted) 290X: + 380X4 5 $1,800 (max dollars spent on radio spots) X1, X2, X3, X420 The solution done in QM results in the following tables: RHS Dual 30 SEC RADIO 2400 0 0 1 MIN RADIO 2800 0 0 5 2718.75 0 Maximize MAX TV SPOTS MAX NEWSPAPER MAX 30 SEC RADIO MAX 1 MIN RADIO WEEKLY ADV BUDGET MIN RADIO SPOTS MAX $ FOR RADIO Solution-> 1 MIN NEWSPAPER TV ADS 5000 8500 1 0 0 0 800 925 0 0 0 1.96885 AMAAAAA 290 8000 6.25 380 2.0259 290 6.2069 1800 67240.3 0 Variable Value 1.9688 1 MIN TV NEWSPAPER ADS 30 SEC RADIO 1 MIN RADIO RANGING TABLE Reduced Cost Original Val Lower Bound Upper Bound 0 5000 0 6620.689 8500 5781.25 Infinity 0 2400 2136.842 Infinity 3 44.8276 2800 - Infinity 3144.828 6.2069 0 Constraint Original Val 12 25 MAX TV SPOTS MAX NEWSPAPER MAX 30 SEC RADIO MAX 1 MIN RADIO WEEKLY ADV BUDGET MIN RADIO SPOTS MAX $ FOR RADIO Dual Value Slack/Surplus 0 10.0313 2718.75 0 0 18.7931 0 20 6.25 0 0 1.2009 2.02590 Lower Bound Upper Bound 1.9688 Infinity 0 6.7027 6.2069 Infinity 0 inity 6425 16025 - Infinity 6.2069 1450 3375 20 8000 5 1800 (10) 12. What are the optimal number of 1 minute TV ads, Newspaper ads, 30 sec Radio ads and 1 min Radio adds to buy and what is the maximum audience coverage from this solution? (10) 13. What constraints are active meaning that all of that resource is used in the optimal solution? (10) 14. For the weekly advertising budget, how much will audience coverage increase if we add $4,000 to that budget and what will be the maximum audience coverage with this new budget? (10) 15. What is the maximum $ amount to which we can increase the weekly advertising budget before the optimal solution changes to a new corner point? What would be the audience coverage at this maximum weekly advertising budget? (10) 16. How much can we increase audience coverage if we increase the number of TV Spots from 12 to 15? (10) 17. The tour manager thinks we should include some 1 minute radio ads in the solution. What would be the effect on the audience coverage if we decided to insert one 1 minute radio add into the solution