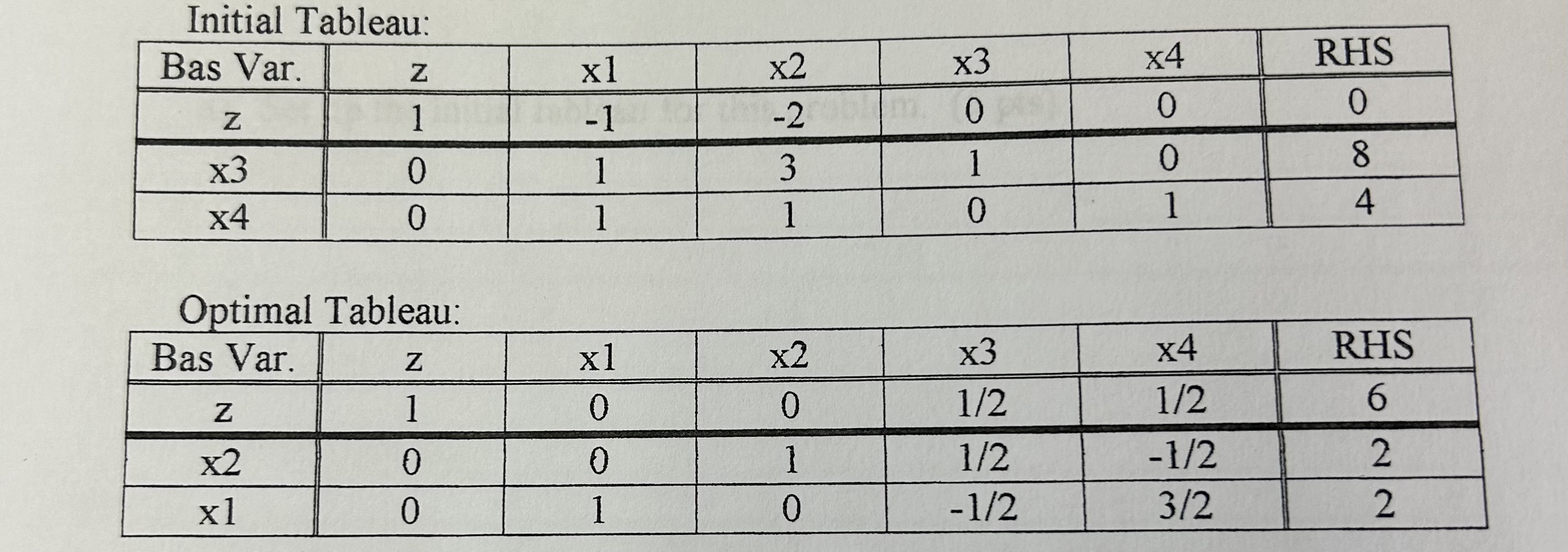
Question: Consider the following LP problem and the corresponding simplex tableaus. Max x1 + 2x2 s.t x1 + 3x2 x1 + x2 x1, x2 >= 0

Consider the following LP problem and the corresponding simplex tableaus.

Max x1 + 2x2

s.t x1 + 3x2

x1 + x2

x1, x2 >= 0

a) At what rate in what direction will the optimal objective function value change as b1 decreases?

b) Suppose a new variable, say x5, is added to the problem. Its objective coefficient is 4, coefficient in constrain 1 is 4, and coefficient in constraint 2 is 2.

i. Does this cause the original optimal solution to be infeasible? Explain.

ii. Does this cause the original optimal solution to be suboptimal (but still feasible)? Explain.

c) Suppose the value of c2 is changed. Indicate whether x2 is basic or nonbasic in the final solution and circle the numbers in the final tableau that will change because of the change in c2.

Consider the following LP problem and the

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Consider the following LP problem: MAX: 2X1 + 4X2 Subject to: -X1 + 2X2 8 X1 + 2X2 12 X1 + X2 2 X1, X2 0 a. Use slack variables to rewrite this problem so that all its constraints are equal to...

Consider the following LP problem. max z = 4x1 + x2 s.t. 3x1 + x2 = 3 4x1 + 3x2 6 x1 + 2x2 4 x1, x2 0 (a) (5 points) Write it in the standard from. (b) (20 points) Using Big-M method, construct the...

Consider the following LP problem and its optimal final tableau shown below: (LP): max z = 2x1 + x2-x3 Basic x1 x2 x3 x4 x5 RHS Z 0 3 xl 1 2 1 x5 0 3 -1 x4 and x5 are slack variables in the 1".., and...

a) (4 points) Suppose that the coefficient of x2 in the objective function is changed from 1 to 6. Does the current bfs remain optimal? If not, just name the entering variable (no need to do simplex...

Question 3. (40 points): Consider the following LP: max z = 3x1 +7x2 +5x3 x s.t. x1 +x2 +x3 +x4 2x1 +3x2 +x3 = 50, X1, X2, X3, X4, X5 0. +x5 = 100, After using the simplex method to solve it, we...

Consider the following LP model: Max z= 5x1 + 4x2 + x3 s.t. x1 + x2 + x3 50 2x1 - x2 + x3 15 x1 + x2 = 10 x1 0, x2 urs, x3 0 a) (6 points) Write the dual problem. b) (3 points) If the primal problem...

4. (30 points) Consider the following LP: max z = 2x- 4x2 + 5x3 - 6x4 s.t. x1 + 4x2 - 2x3 + 8x4 2 -x1 + 2x2 + 3x3 + 4x4 1 X1, X2, X3, X4 0 Find the optimum solution using the revised simplex method.

Consider the following problem. Maximize Z 2x1 x2 4x3 3x4, subject to x1 x2 3x3 2x4 4 x1 x2 x3 x4 1 2x1 x2 x3 x4 2 x1 2x2 x3 2x4 2 and x2 0, x3 0, x4 0 (no nonnegativity constraint...

2. Consider the following LP problem. Formulate the problem using Big M method. Maximize Z = 5X1 + 6X2 s.t. -2X1 + 3X2 = 3 4X1 + 8 X2 25 X1 + 2X2 s 14 X1, X2 20 What is the equivalent annual cost in...

Problem 1. Consider the following LP. min 2x1 - x2 + 3x3 X1 X2 s.t. X1 + x2 + x3 3 2x2 + 2x2 + x3 59 X-X2 - 2x3 20 X 55 X1 2 0,X, S 0,X3 20 1) Write the standard form of this LP. (10 points) 2) Write...

what are immediate implications of ratio analysis of A what are long term analysis of ratio a D1 1 RATIO 2 LIQUIDITY 3 CURRENT 4 QUICK 5 ASSET MANAGEMENT 6 INVENTORY TURNOVER DAYS SALE OUTSTANDING...

Psychologists define implicit self-esteem as unconscious evaluations of ones worth or value. In contrast, explicit self-esteem refers to the extent to which a person consciously considers oneself as...

Which of the following is an example of systematic risk? a . The national trade deficit is higher than expected b . A compamy announces a incumbernt CEO's departure. c . A company has been hit by a...

On September 1st, 2018, Mr. Payton moves from Sudbury to Ottawa (Ottawa is 484 kilometers from Sudbury)for a new job. He lived in a rented apartment in Sudbury and purchased a house in Ottawa. The...