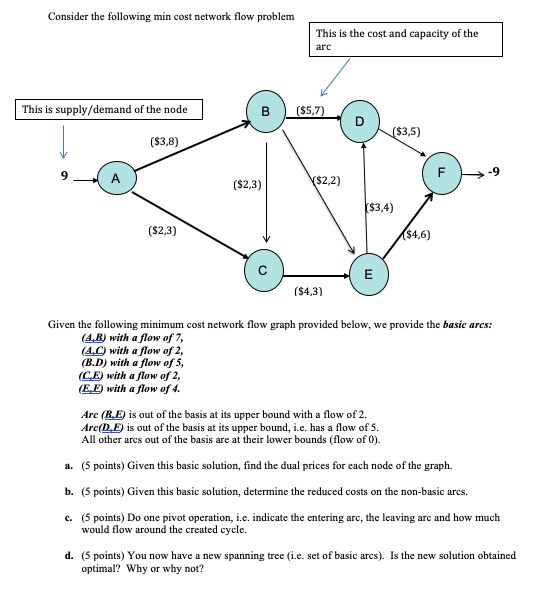
Consider the following min cost network flow problem This is the cost and capacity of the arc This is supply/demand of the node B ($5,7) ($3,5) ($3,8) F A ($2,3) $2,2) ($3,4) ($2,3) (54,6) E ($4,3) Given the following minimum cost network flow graph provided below, we provide the basic arcs: (4.B) with a flow of 7, (4,0 with a flow of 2 (B.D) with a flow of 5, (CE) with a flow of 2, (E.D with a flow of 4. Arc (BE) is out of the basis at its upper bound with a flow of 2. ArcD.E) is out of the basis at its upper bound, i.e. has a flow of 5. All other ares out of the basis are at their lower bounds (flow of 0). a. (5 points) Given this basic solution, find the dual prices for each node of the graph. b. (5 points) Given this basic solution, determine the reduced costs on the non-basic arcs. C. (5 points) Do one pivot operation, i.e. indicate the entering arc, the leaving arc and how much would flow around the created cycle. d. (5 points) You now have a new spanning tree (i.c. set of basic arcs). Is the new solution obtained optimal? Why or why not? Consider the following min cost network flow problem This is the cost and capacity of the arc This is supply/demand of the node B ($5,7) ($3,5) ($3,8) F A ($2,3) $2,2) ($3,4) ($2,3) (54,6) E ($4,3) Given the following minimum cost network flow graph provided below, we provide the basic arcs: (4.B) with a flow of 7, (4,0 with a flow of 2 (B.D) with a flow of 5, (CE) with a flow of 2, (E.D with a flow of 4. Arc (BE) is out of the basis at its upper bound with a flow of 2. ArcD.E) is out of the basis at its upper bound, i.e. has a flow of 5. All other ares out of the basis are at their lower bounds (flow of 0). a. (5 points) Given this basic solution, find the dual prices for each node of the graph. b. (5 points) Given this basic solution, determine the reduced costs on the non-basic arcs. C. (5 points) Do one pivot operation, i.e. indicate the entering arc, the leaving arc and how much would flow around the created cycle. d. (5 points) You now have a new spanning tree (i.c. set of basic arcs). Is the new solution obtained optimal? Why or why not