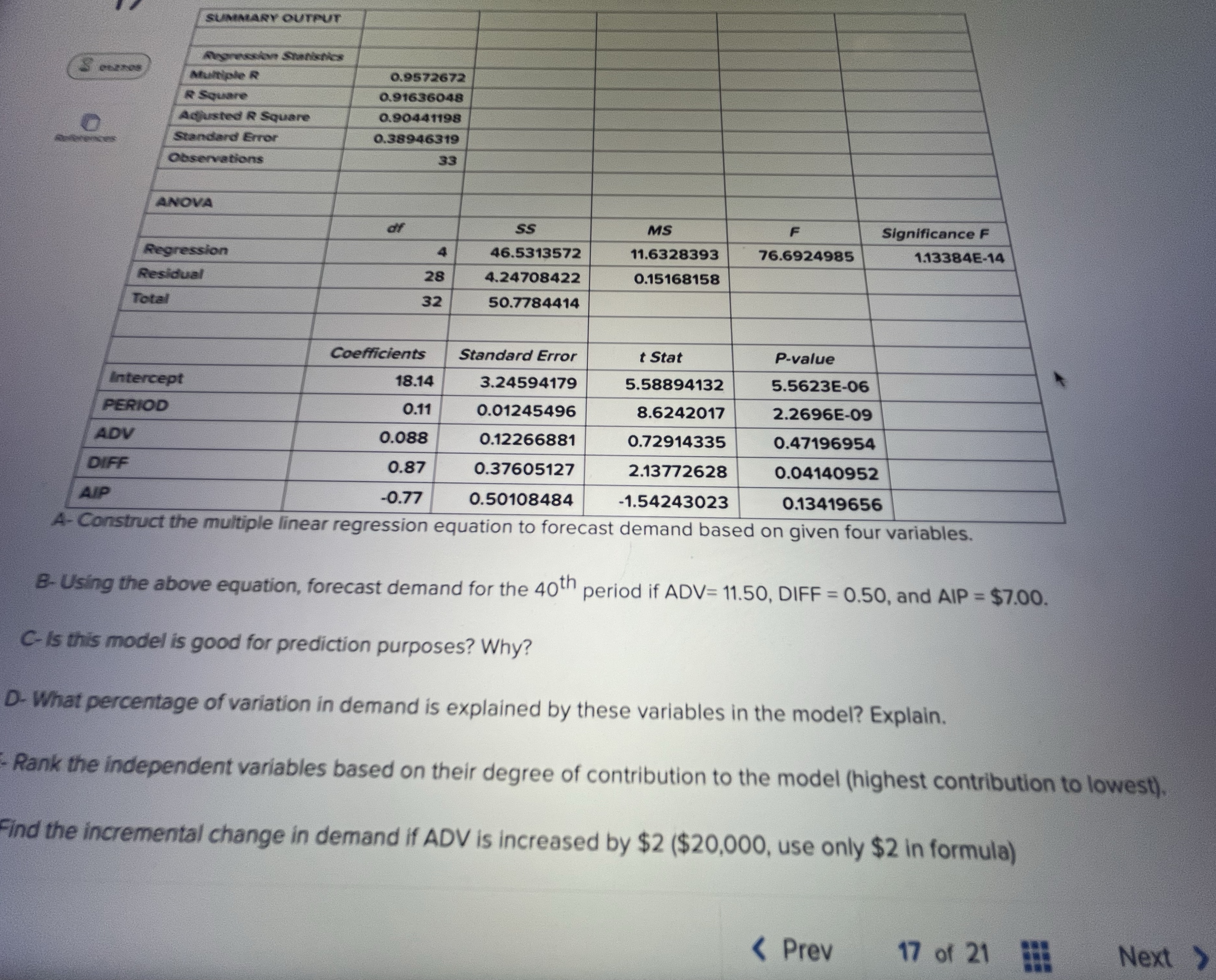
Question: Consider the following Multiple linear regression output to predict demand (in 100,000 units) for a product given variables Period, ADV(I0,000), DIFF($), and AIP ($). SUMMARY
Consider the following Multiple linear regression output to predict demand (in 100,000 units) for a product given variables Period, ADV(I0,000), DIFF($), and AIP ($).
SUMMARY OUTPUT Agreeson Statistics Multiple R 0.9572672 R Square 0.91636048 Adjusted R Square 0.90441198 Standard Error 0.38946319 observations 33 ANOVA df SS MS Significance F Regression 4 46.5313572 11.6328393 76.6924985 1.13384E-14 Residual 28 4.24708422 0.15168158 Total 32 50.7784414 Coefficients Standard Error t Stat P-value Intercept 18.14 3.24594179 5.58894132 5.5623E-06 PERIOD 0.11 0.01245496 8.6242017 2.2696E-09 ADV 0.088 0.12266881 0.72914335 0.47196954 DIFF 0.87 0.37605127 2.13772628 0.04140952 AIP -0.77 0.50108484 -1.54243023 0.13419656 A- Construct the multiple linear regression equation to forecast demand based on given four variables. B- Using the above equation, forecast demand for the 40' period if ADV= 11.50, DIFF = 0.50, and AIP = $7.00. C- Is this model is good for prediction purposes? Why? D- What percentage of variation in demand is explained by these variables in the model? Explain. Rank the independent variables based on their degree of contribution to the model (highest contribution to lowest). Find the incremental change in demand if ADV is increased by $2 ($20,000, use only $2 in formula)