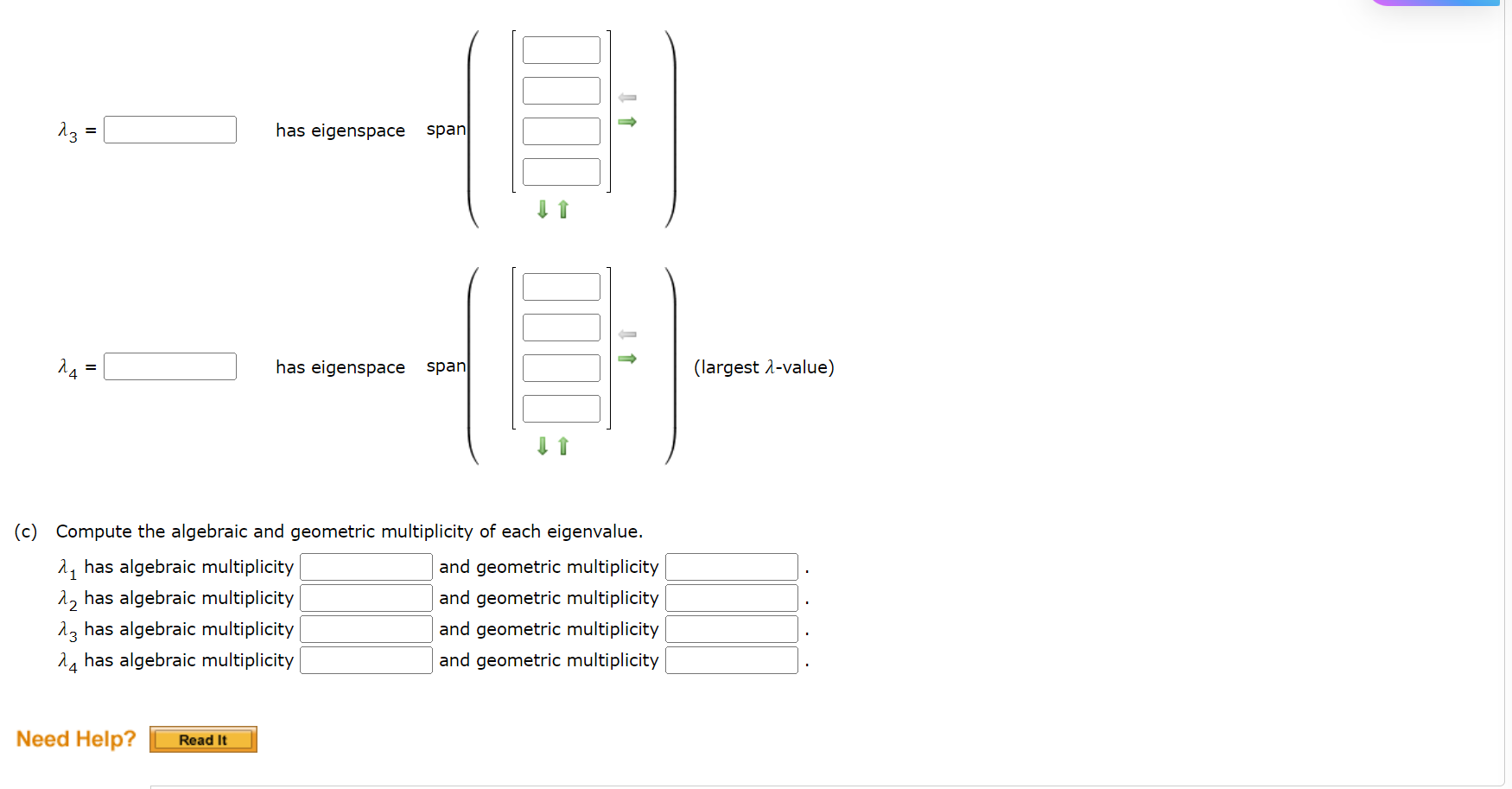
Consider the following. O. Summary + 9 01 0 A = 0 9 0 01 7 0 0 0 (a) Compute the characteristic polynomial of A. det(A - AI) = (b) Compute the eigenvalues and bases of the corresponding eigenspaces of A. (Repeated eigenvalues should be entered repeatedly with the same eigenspaces.) My = has eigenspace span (smallest )-value) 12 = has eigenspace spanA3 = E has eigenspace span mm -_ : (largest -value) ll4 = :l has eigenspace span mm c: I: (c) Compute the algebraic and geometric multiplicity of each eigenvalue. 111 has algebraic multiplicity : and geometric multiplicity :. 112 has algebraic multiplicity : and geometric multiplicity :. 113 has algebraic multiplicity :] and geometric multiplicity :l. l4 has algebraic multiplicity : and geometric multiplicity :. Need Help? Show that A and B are not similar matrices. A = Since A has characteristic polynomial p(1) = and B has characteristic polynomial p(1) = the two matrices are not similar. Need Help? Read ItShow that A and B are not similar matrices. (Enter your answers as comma-separated lists. ) O. Summary + 4 1 8 1 0 0 A = 047 B = -1 8 0 0 0 8 4 7 8 Since A has eigenvalues 1 = and B has the eigenvalues 1 = , the two matrices are not similar. Need Help? Read It