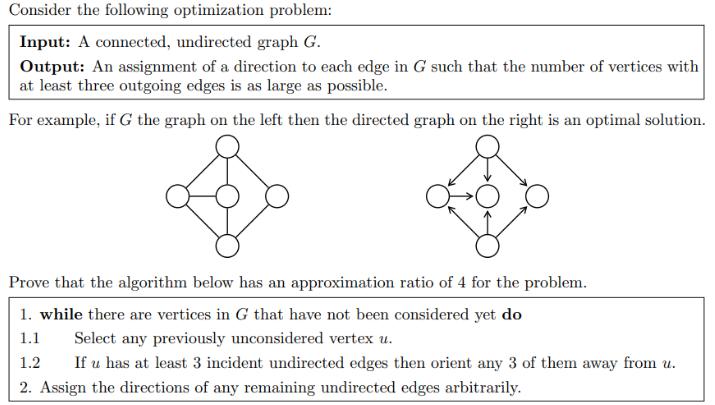
Consider the following optimization problem: Input: A connected, undirected graph G. Output: An assignment of a direction to each edge in G such that the number of vertices with at least three outgoing edges is as large as possible. For example, if G the graph on the left then the directed graph on the right is an optimal solution. Prove that the algorithm below has an approximation ratio of 4 for the problem. 1. while there are vertices in G that have not been considered yet do 1.1 Select any previously unconsidered vertex u. 1.2 If u has at least 3 incident undirected edges then orient any 3 of them away from u. 2. Assign the directions of any remaining undirected edges arbitrarily.