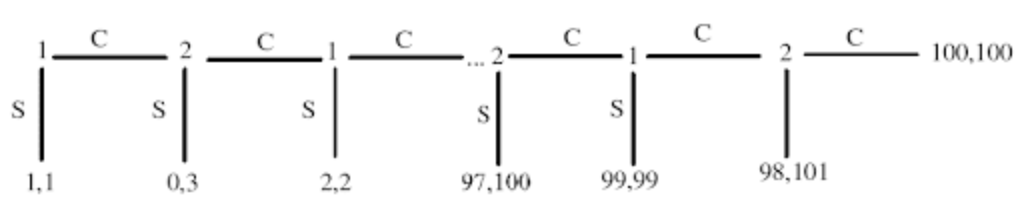
Consider the following sequential-move game. The game begins with 2 dollars on the table -- player 1 can either stop, in which case they split the money, or continue, in which case a dollar is added to the plate. Now, player 2 can choose to stop, get 3 dollars, or continue, in which case a dollar is added, and 1 can stop, which gives now 2 dollars each, or continue, in which case a dollar is added, player 2 can stop, giving $1 to player 1, $4 to himself, or continue, in which case again a dollar is added, and so on, until in the final round, player 2 can either stop, in which case player 1 gets $98 and player 2 gets $101, or continue, in which case they both receive $100. Solve for the subgame-perfect Nash equilibrium of the game.