Consider the following sum S_n:

S_n = 2² log 2 + 3² log 3 + + n² log n, where the base of the logarithms is e:

(i) From the theory in class, lower and upper bounds on S_n can be obtained by using the following formula with some function f(x).

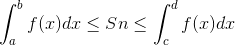
State an appropriate function f(x) and values of limits a, b, c, d:

f(x) = _______________ , a = _______, b = ________, c = ________, d = _________.

(ii) Is f(x) non-increasing or non-decreasing for large n? _____________.

(iii) Now integrate and obtain lower and upper bounds on S_n .

(iv) Obtain the ?-complexity of S_n .