Consider the following variation on the Interval Scheduling Problem. You have a proces- sor that can operate 24 hours a day, every day. People submit requests to run daily jobs on the processor. Each such job comes with a start time and an end time; if the job is accepted to run on the processor, it must run continuously, every day, for the period between its start

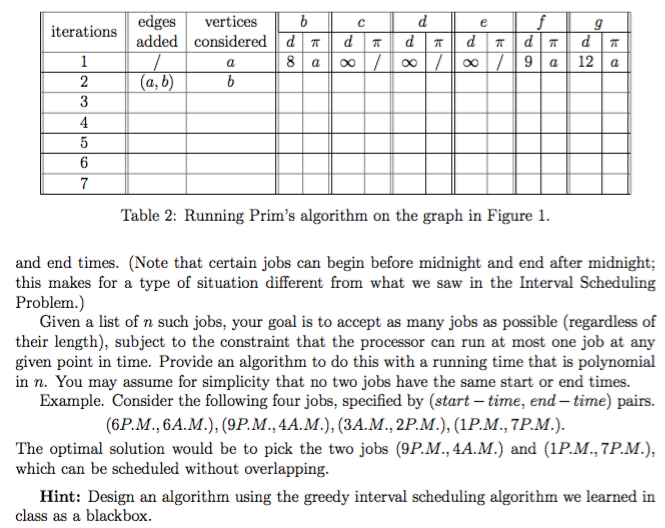
edges vertices iterations added considered d T d T d T d T T T OOD 9 a 12 a Table 2: Running Prim's algorithm on the graph in Figure 1. and end times. (Note that certain jobs can begin before midnight and end after midnight; this makes for a type of situation different from what we saw in the Interval Scheduling Problem. Given a list of n such jobs, your goal is to accept as many jobs as possible regardless of their length), subject to the constraint that the processor can run at most one job at any given point in time. Provide an algorithm to do this with a running time that is polynomial in n. You may assume for simplicity that no two jobs have the same start or end times Example. Consider the following four jobs, specified by (start-time, end-time) pairs. (6PM., 6A.M.), (9 P.M., 4A.M.), (3A.M., 2PM.), (1PM.,7PM.) The optimal solution would be to pick the two jobs (9PM., 4A.M.) and (1P.M.,7PM.), which can be scheduled without overlapping. Hint: Design an algorithm using the greedy interval scheduling algorithm we learned in class as a blackbox