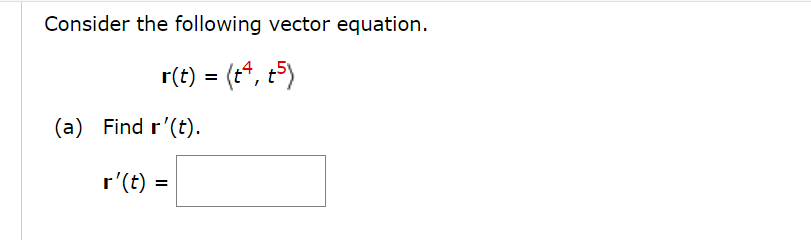
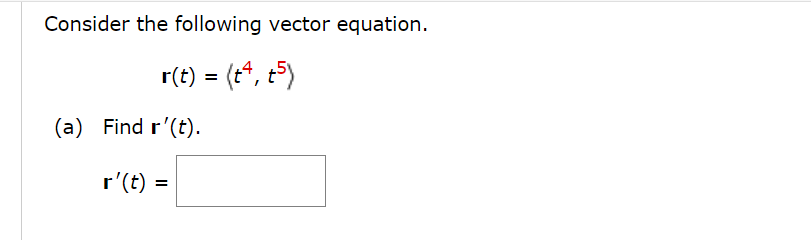
Question: Consider the following vector equation. r(t) = (+4, + 5) (a) Find r'(t). r'(t) =2. [-/1 Points] DETAILS SCALC9 13.2.010. Find the derivative, r'(t), of
![Find r'(t). r'(t) =2. [-/1 Points] DETAILS SCALC9 13.2.010. Find the derivative,](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66611b504d2ca_01666611b503fc06.jpg)

![r'(t) = Need Help? Read It 3. [0/1 Points] DETAILS PREVIOUS ANSWERS](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66611b50d6214_01666611b50c6010.jpg)





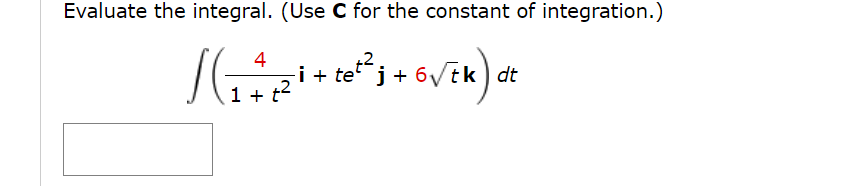

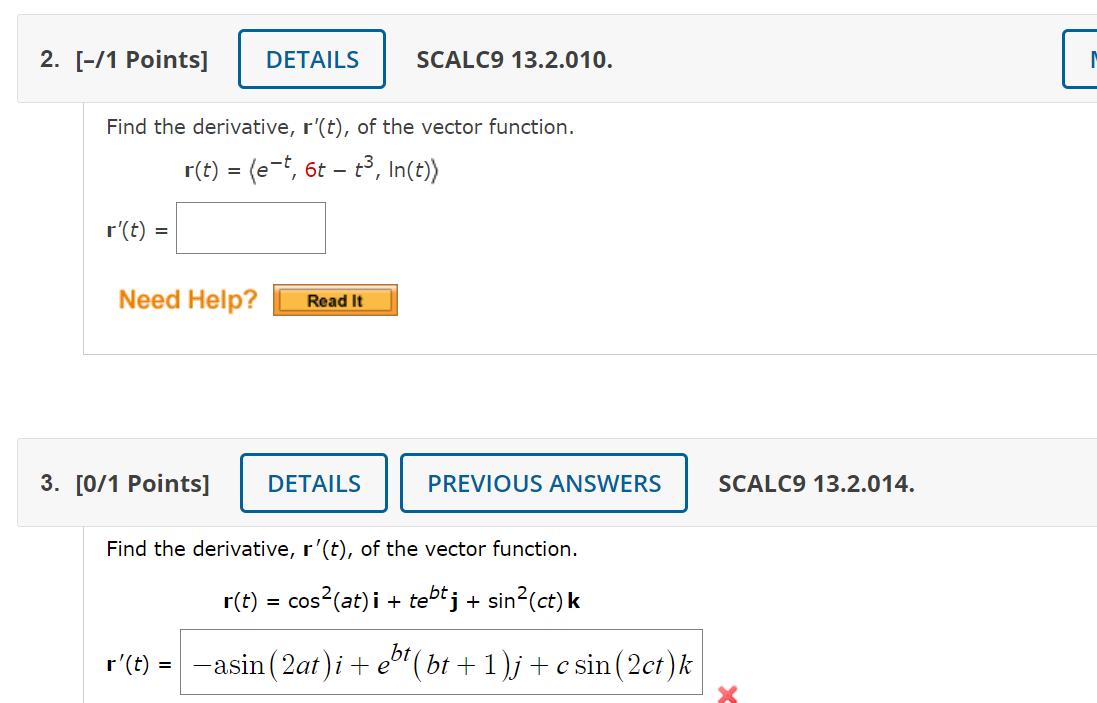

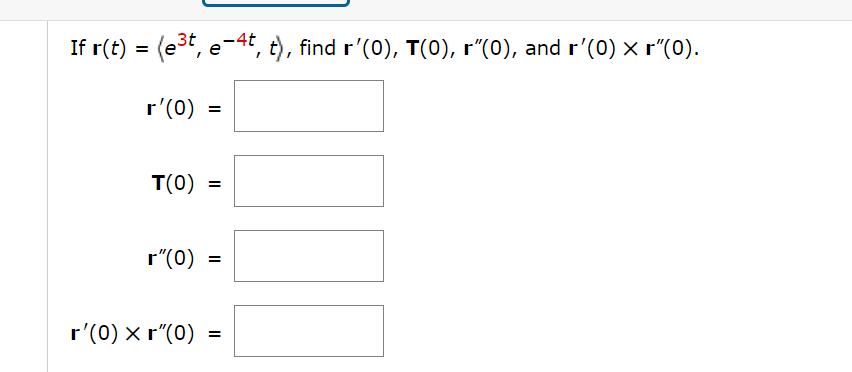





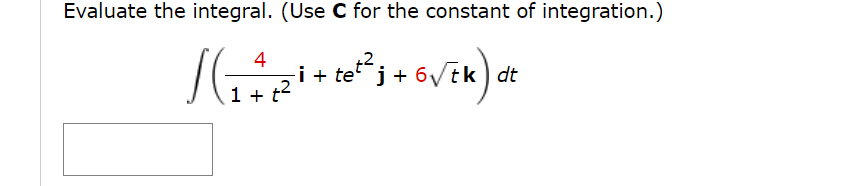

Consider the following vector equation. r(t) = (+4, + 5) (a) Find r'(t). r'(t) =2. [-/1 Points] DETAILS SCALC9 13.2.010. Find the derivative, r'(t), of the vector function. r(t) = (e-t, 6t - ts, In(t)) r'(t) = Need Help? Read It 3. [0/1 Points] DETAILS PREVIOUS ANSWERS SCALC9 13.2.014. Find the derivative, r'(t), of the vector function. r(t) = cos2(at) i + tebt; + sin2(ct) k r '(t) = -asin (2at )i + ebt (bt + 1 )j + csin(2ct ) k XFind the unit tangent vector T(t) at the point with the given value of the parameter r. r(t) = (tan1U), 3e2t, 18tet}, t = 0 1(0) = If r(t) = (e3t -4t , t) , find r'(0), T(0), r"(0), and r'(0) X r"(0). r'(0) = T(0) = r"(0) = r'(0) X r"(0) =Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. X = V t2 + 63, y = In(+2 + 63), z = t; (8, In(64), 1) x (t ) , y (t ), z (t ) ) =Find the point on the curve r(t) = (8 cos(t), 8 sin(t), er), 0 S t 5 31', where the tangent line ls parallel to the plane "Ex + y = 1. (XMZ) =( ) rind parametric equations for the tangent line to the curve with the given parametric equations at the specified point. X = 10 cos(t), y = 10 sin(t), z = 2 cos(2t), (EVE, 5, 1) x0), ya), 2(0) =( ) Evaluate the integral. T/4 (sec(t) tan(t) i + t cos(2t) j + sin-(2t) cos(2t) k) dt JoEvaluate the integral. (Use C for the constant of integration.) 4 i + tej + 6\ tk dt 1+ +2
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


