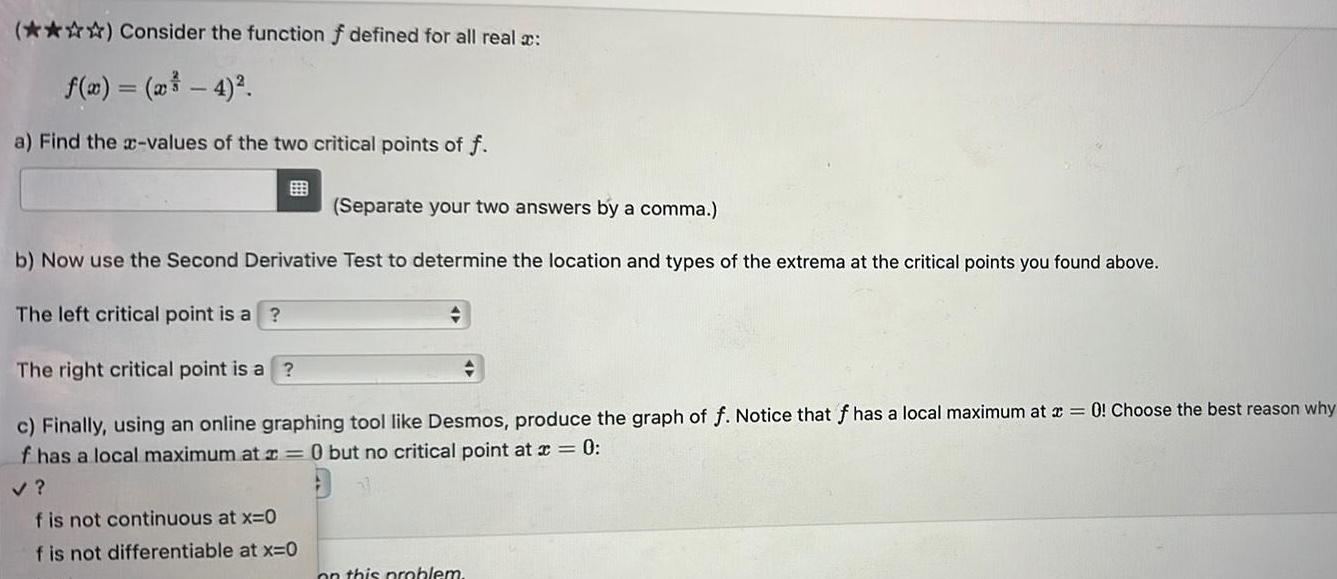
(***) Consider the function f defined for all real: f(x) = (x-4). a) Find the z-values of the two critical points of f. (Separate your two answers by a comma.) b) Now use the Second Derivative Test to determine the location and types of the extrema at the critical points you found above. The left critical point is a ? The right critical point is a ? c) Finally, using an online graphing tool like Desmos, produce the graph of f. Notice that f has a local maximum at 20! Choose the best reason why f has a local maximum at x= 0 but no critical point at x = 0: ? f is not continuous at x=0 f is not differentiable at x=0 on this problem.