Question: Consider the function f : IR -> R defined by f(x) = -' + 6. Let / = [-5, 1). Describe the following sets as
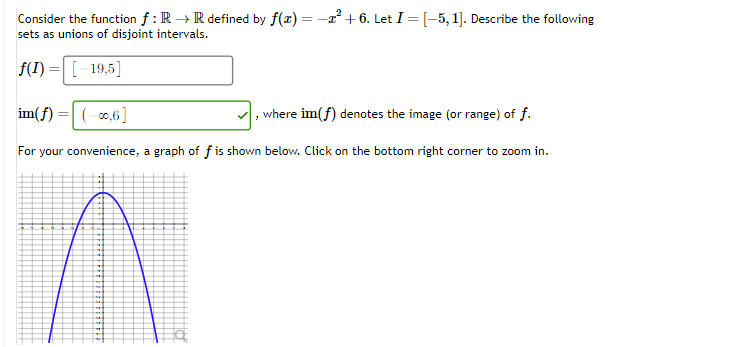

![sets as unions of disjoint intervals. f(I) = [-19,5] im( f) =](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6709062375566_6436709062363d98.jpg)
![(-00,6 ] , where im(f) denotes the image (or range) of f.](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67090623e8c91_64367090623c72d7.jpg)
Consider the function f : IR -> R defined by f(x) = -' + 6. Let / = [-5, 1). Describe the following sets as unions of disjoint intervals. f(I) = [-19,5] im( f) = (-00,6 ] , where im(f) denotes the image (or range) of f. For your convenience, a graph of f is shown below. Click on the bottom right corner to zoom in.Consider the function f : R - Z, f(x) = [x] (the floor of @). Describe the following set using the roster method, where I = (-1, 6]. f(I) Now consider the function g : R - Z, f(x) = [x] (the ceiling of x). Describe the following set using the roster method, where J = [-9, -1). 9 ( J) =Find the smallest set B C IR such that the assignment f(I) = 4r' - 161 +9 defines a function f : IR - B. Write your answer as a union of disjoint intervals.Let A = {2,3,5,6,14,17, 19, 20} and consider the function f: A & with graph {(2,6),(3,4),(5,7),(6,8), (14,4), (17,0), (10,1), (20, 4)}. Find a set C A of the largest possible cardinality such that the restriction of f to is an injective function. 5=
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


