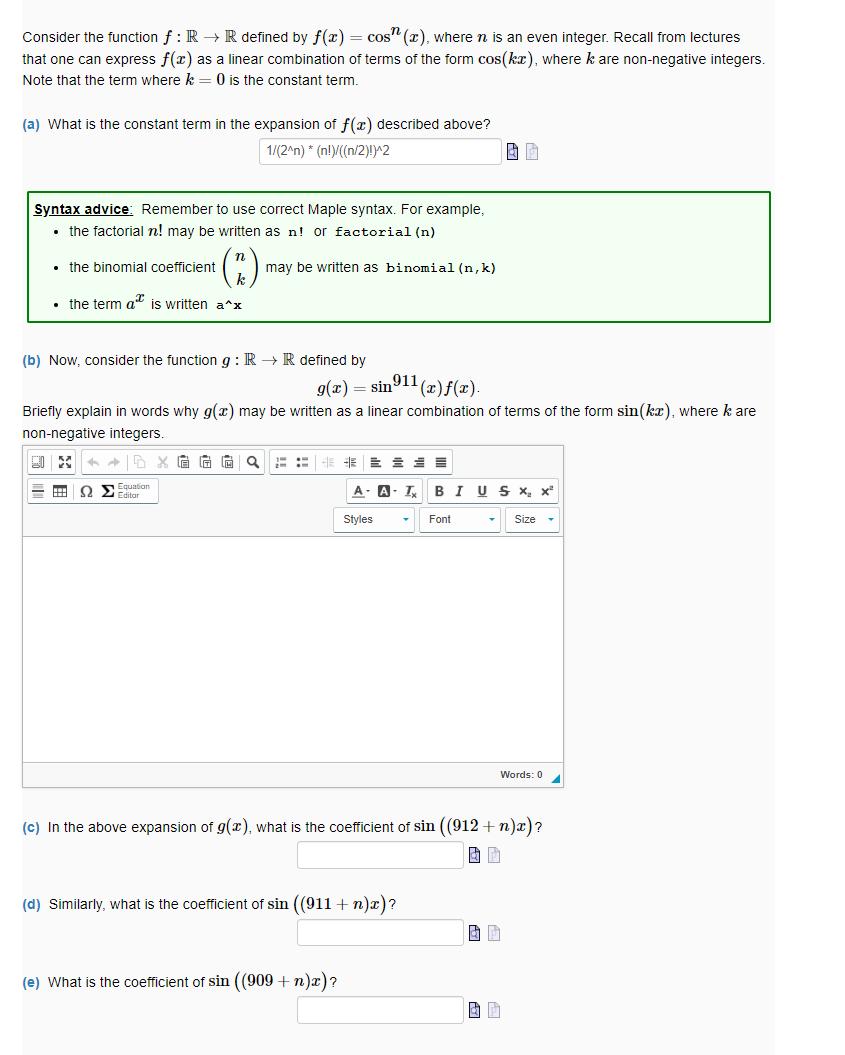
Consider the function f: RR defined by f(x) = cos(x), where n is an even integer. Recall from lectures that one can express f(x) as a linear combination of terms of the form cos(kx), where k are non-negative integers. Note that the term where k = 0 is the constant term. (a) What is the constant term in the expansion of f(x) described above? 1/(2^n) * (n!)/((n/2)!)^2 Syntax advice: Remember to use correct Maple syntax. For example, the factorial n! may be written as n! or factorial (n) the binomial coefficient (*) may be written as binomial (n,k) k the term a is written a^x (b) Now, consider the function g: R R defined by 9(x)=sin911(x) f(x). Briefly explain in words why g(x) may be written as a linear combination of terms of the form sin(kx), where k are non-negative integers. DX Equation Editor A-AI BI U S x, x* Styles Font Size Words: 0 (c) In the above expansion of g(x), what is the coefficient of sin ((912 + n)x)? (d) Similarly, what is the coefficient of sin ((911+ n)x)? (e) What is the coefficient of sin ((909 + n)x)?