Question: Consider the function f ( x ) = x + 6 x ^ 2 / 3 ( f ) Give the inflection points of f
Consider the function fx x x
f Give the inflection points of fx
Enter your answers in increasing order of the xcoordinate. If there are less than two points of
inflection, enter NA in the remaining response areas.
Include a multiplication sign between symbols. For example, apic Give the intervals of increase and decrease of fx
Note: Use the letter U for union. To enter infty type infinity with a lower case i
If the function is never increasing or decreasing, enter NA in the associated response area.
increasing:
decreasing:
c Give the intervals of increase and decrease of fx
Note: Use the letter U for union. To enter infty type infinity with a lower case i
If the function is never increasing or decreasing, enter NA in the associated response area.
increasing:
decreasing:
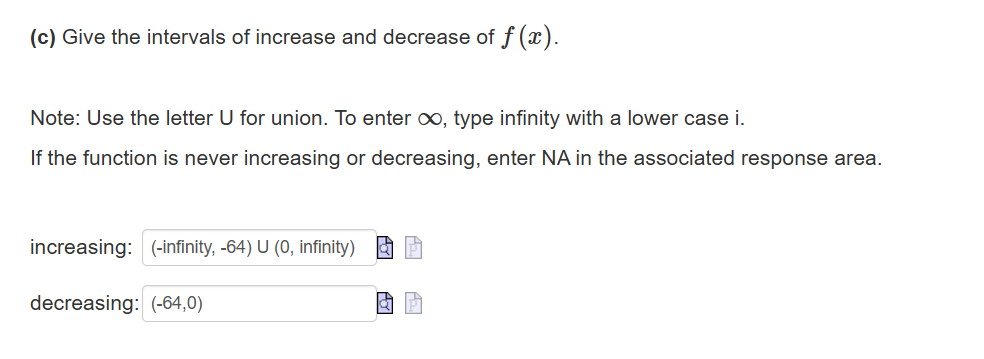
c Give the intervals of increase and decrease of fx
Note: Use the letter U for union. To enter infty type infinity with a lower case i
If the function is never increasing or decreasing, enter NA in the associated response area.
increasing:
decreasing:
d Give the local maximum and minimum values of fx
Enter your answers in increasing order of the x value. If there are less than two local extrema enter NA in the remaining response areas and the corresponding dropdown menu.
Include a multiplication sign between symbols. For example, a cdot pi e Give the intervals of concavity of fx
Note: Use the letter U for union. To enter infty type infinity with a lower case i
If the function is never concave upward or concave downward, enter NA in the associated response area.
concave
upward:
concave
downward:
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


