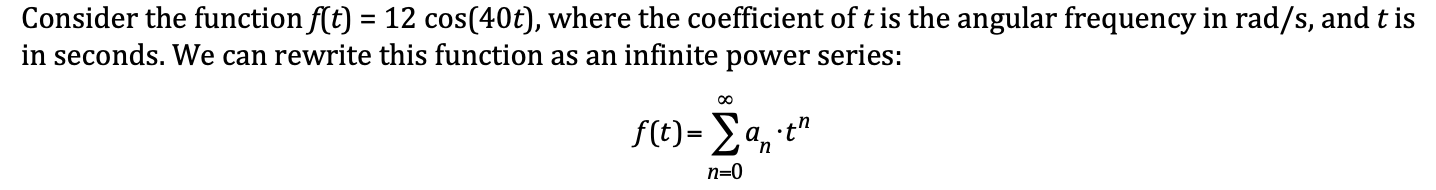
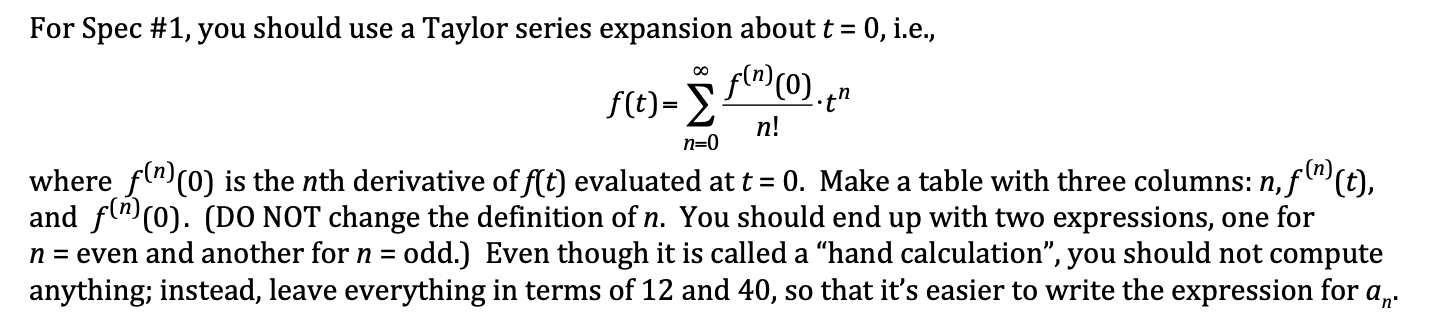
Consider the function f{t) = 12 cos(40t), where the coefficient of t is the angular frequency in rad/s, and t is in seconds. We can rewrite this function as an infinite power series: f)= Y a,t" n=0 For Spec #1, you should use a Taylor series expansion about t =0, i.e., > f(n) flt)= Ef |[0] g = n where (M(0) is the nth derivative of f(t) evaluated at t = 0. Make a table with three columns: n, f (")(t), and ("(0). (DO NOT change the definition of n. You should end up with two expressions, one for n = even and another for n = odd.) Even though it is called a \"hand calculation\