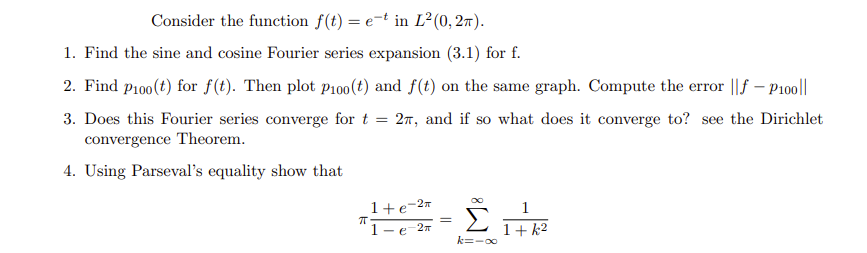
Consider the function f(t) = e t in 12 (0, 2x). 1. Find the sine and cosine Fourier series expansion (3.1) for f. 2. Find Pioo(t) for f(t). Then plot Pioo(t) and f(t) on the same graph. Compute the error |If - Pooll 3. Does this Fourier series converge for t = 27, and if so what does it converge to? see the Dirichlet convergence Theorem. 4. Using Parseval's equality show that 1+e-2x DO 1 "1 - e- 2x 1 + 12 *=-00